
 ��ͼ��ʾ����ֱ���õ����˷�յIJ�������ע����ˮ������һ������������ˮ�������ϸ����ں�����Ӳ����ܵ��¶������ϸ���ͬʱ��ʹ���������ٶ�vˮƽ���������˶�����֪���������������ٶȴ�СΪ3cm/s��������ˮƽ�˶����ٶȴ�СΪ4cm/s����
��ͼ��ʾ����ֱ���õ����˷�յIJ�������ע����ˮ������һ������������ˮ�������ϸ����ں�����Ӳ����ܵ��¶������ϸ���ͬʱ��ʹ���������ٶ�vˮƽ���������˶�����֪���������������ٶȴ�СΪ3cm/s��������ˮƽ�˶����ٶȴ�СΪ4cm/s����| A������ֱ���˶� | B���ȱ���ֱ���˶� | C�������˶� |
���� ��1���������������ֱ�����������ϵ��˶�������Ӷ���֪����˶���ֱ���˶���������ֱ���˶����ȱ���ֱ���˶������������˶���
��2������ˮƽ����ֱ�����ϵ��ٶȣ���������ƽ���ı��ζ�����кϳɣ����������ʵ���˶����ٶȣ�
��� �⣺��1�����������ˮƽ�����ϵ�����ֱ���˶�����ֱ�����ϵ�����ֱ���˶��������������ϵ��˶��ļ��ٶȶ�Ϊ�㣬���Ժϼ��ٶȷ���Ϊ�㣬����������ֱ���˶���ѡ��A��ȷ��
��ѡ��A
��2��������˶����ٶ�Ϊ��v��=$\sqrt{{v}_{������}^{2}+{v}_{����}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5cm/s
�ʴ�Ϊ����1��A�� ��2��5
���� ���⿼���˺�ʸ�����ʸ��֮��Ĺ�ϵ���ڽ���ʸ���ĺϳ�ʱ������Ҫ�ж�����ͬһ��ֱ���ϣ����Dz���ͬһ��ֱ���ϣ���ͬһ��ֱ����ʱ�����ô����ͽ��з����ͼ��㣬����ͬһ��ֱ����ʱ������ƽ���ı��ζ�����з����ͼ��㣮���о��Ƕ����˶���ʽ���жϣ���ͨ�����ٶ��Ƿ�Ϊ�����ٶȲ�Ϊ��ʱ�����ٶ�����ٶ��Ƿ���ͬһ��ֱ�������ж���������ֱ���˶����������˶���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | UI | B�� | UI-I2R | C�� | UI+I2R | D�� | $\frac{{U}^{2}}{R}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
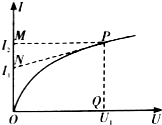 ij����Ԫ��ͨ��������I�����ӵ�ѹU�仯��ͼ����ͼ��ʾ��PΪͼ����һ�㣬PNΪͼ�ߵ����ߣ�PQΪU��Ĵ��ߣ�PMΪI��Ĵ��ߣ�����˵������ȷ���ǣ�������
ij����Ԫ��ͨ��������I�����ӵ�ѹU�仯��ͼ����ͼ��ʾ��PΪͼ����һ�㣬PNΪͼ�ߵ����ߣ�PQΪU��Ĵ��ߣ�PMΪI��Ĵ��ߣ�����˵������ȷ���ǣ�������| A�� | �������ӵ�ѹ������Ԫ���ĵ������� | |
| B�� | ��ӦP�㣬��Ԫ���ĵ���ΪR=$\frac{{U}_{1}}{{I}_{1}}$ | |
| C�� | ��ӦP�㣬��Ԫ���ĵ���ΪR=$\frac{{U}_{1}}{{I}_{2}-{I}_{1}}$ | |
| D�� | ��Ԫ��Ϊ������Ԫ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������ǵİ뾶��� | B�� | �������ǵ��ܶ���� | ||
| C�� | �������ǵ�������� | D�� | �������ǵ����ٶȴ�С��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �������ͬ������ʱ���Ƚ����Ƿ���������Բ�ι��1��Ȼ���ʹ������Բ���2���У�����ٴε����������ͬ�����3�����1��2������A�㣬���2��3������B�㣬��ͼ��ʾ�������Ƿֱ���1��2��3�������������ʱ������˵����ȷ���ǣ�������
�������ͬ������ʱ���Ƚ����Ƿ���������Բ�ι��1��Ȼ���ʹ������Բ���2���У�����ٴε����������ͬ�����3�����1��2������A�㣬���2��3������B�㣬��ͼ��ʾ�������Ƿֱ���1��2��3�������������ʱ������˵����ȷ���ǣ�������| A�� | �����ڹ��1�ϵĻ�е�ܵ��ڹ��3�ϵĻ�е�� | |
| B�� | �����ڹ��1�ϵ����ڵ����ڹ��2�ϵ����� | |
| C�� | ��������Բ���1�ϵļ��ٶȴ������ڹ��3�ϵļ��ٶ� | |
| D�� | ��������Բ���2�Ͼ���A��ʱ���ٶ�С��7.9 km/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ö���ֻ�����ڵ��ɲ����ĵ糡 | |
| B�� | ���ض��ɵı���ʽF=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$����˵�ǵ���q2�����ĵ糡�ڵ���q1���Ŀ�������С����k$\frac{{q}_{1}}{{r}^{2}}$����˵�ǵ���q2�����ĵ糡�ڵ���q1���ij�ǿ��С | |
| C�� | ��E=$\frac{F}{q}$��F�Ƿ���糡�еĵ������ܵľ�������q�Dz����糡�ĵ�ɵĵ���� | |
| D�� | �糡��ij�㳡ǿ�ķ�������̽��ɵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
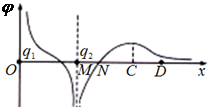 ��������ֱ�Ϊq1��q2�ĵ��ɹ̶���x���ԭ��O������x0��M�㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ������ND��������Ϊ2x0��C�������ߣ�������ļ����ɴ�N���Ƶ�D�㣮�����ж���ȷ���ǣ�������
��������ֱ�Ϊq1��q2�ĵ��ɹ̶���x���ԭ��O������x0��M�㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ������ND��������Ϊ2x0��C�������ߣ�������ļ����ɴ�N���Ƶ�D�㣮�����ж���ȷ���ǣ�������| A�� | q1=2q2 | |
| B�� | q1Ϊ����ɣ�q2Ϊ����� | |
| C�� | �糡���Ըü��������������������� | |
| D�� | �ü����ɵ���C��ʱ�ٶ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com