
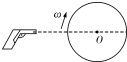
 如图所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口垂直对准愿同轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,则子弹的速度可能是( )
如图所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口垂直对准愿同轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,则子弹的速度可能是( )| A. | $\frac{dω}{π}$ | B. | $\frac{dω}{2π}$ | C. | $\frac{dω}{3π}$ | D. | $\frac{dω}{5π}$ |
分析 子弹沿圆筒直径穿过圆筒,结果发现圆筒上只有一个弹孔,在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,结合角速度求出时间,从而得出子弹的速度.
解答 解:在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,
则时间为:t=$\frac{(2n-1)π}{ω}$,
所以子弹的速度为:
v=$\frac{d}{t}$=$\frac{dω}{(2n-1)π}$,n=1、2、3…
当n=1时,v=$\frac{dω}{π}$
当n=2时,v=$\frac{dω}{3π}$
当n=3时,v=$\frac{dω}{5π}$
所以ACD是可能的,B是不可能的.
故选:ACD
点评 解决本题的关键知道圆筒转动的周期性,结合转过角度的通项式得出运动的时间,抓住子弹飞行的时间和圆筒转动时间相等进行求解.


科目:高中物理 来源: 题型:选择题
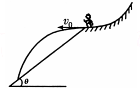 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,运动员落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,运动员落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 运动员刚要落到雪坡上时的速度大小为$\frac{{v}_{0}}{cosθ}$ | |
| D. | 运动员在空中经历的时间为$\frac{2{v}_{0}tanθ}{g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
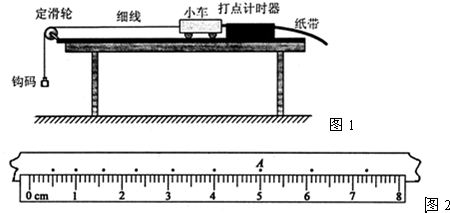
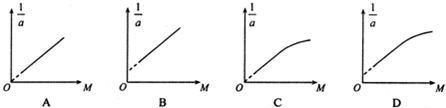
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 甲、乙达到最高点的所需时间之比为1:4 | |
| B. | 甲、乙所能达到的最大高度之比为1:4 | |
| C. | 甲、乙做竖直上抛运动的初速度之比为1:4 | |
| D. | 甲、乙粉笔第一次运动到最高点的一半位移所用时间之比为1:4 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 甲乙两物体在同一直线上运动的x-t图象如图所示,以甲的出发点为原点,出发时刻为计时起点.则从图象可以看出( )
甲乙两物体在同一直线上运动的x-t图象如图所示,以甲的出发点为原点,出发时刻为计时起点.则从图象可以看出( )| A. | t3时刻甲乙速度相等 | |
| B. | 甲乙同时、同地出发 | |
| C. | 甲在中途停了一会儿,但最终也没追上乙 | |
| D. | t2到t3这段时间内甲的平均速度大于乙的平均速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 光滑水平面上静止一质量为m的物体,现用一水平力拉物体,使物体从静止开始运动,物体的加速度随时间变化的关系如图所示,则此物体( )
光滑水平面上静止一质量为m的物体,现用一水平力拉物体,使物体从静止开始运动,物体的加速度随时间变化的关系如图所示,则此物体( )| A. | 在0~2 s内做匀加速直线运动 | B. | 在2 s末的速度为2 m/s | ||
| C. | 在2 s~4 s内的位移为8m | D. | 在t=4 s时速度最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,质量不同的P、Q两球均处于静止状态,现用小锤打击弹性金属片,使P球沿水平方向抛出,Q球同时被松开而自由下落.则下列说法中正确的是( )
如图所示,质量不同的P、Q两球均处于静止状态,现用小锤打击弹性金属片,使P球沿水平方向抛出,Q球同时被松开而自由下落.则下列说法中正确的是( )| A. | P球先落地 | B. | Q球先落地 | ||
| C. | 两球落地时的动能可能相等 | D. | 两球下落过程中重力势能变化相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com