一个质量为m带电量为+q的小球，每次均以初速度v0水平向右抛出，抛出点距离水平地面的高度为h，不计空气阻力，重力加速度为g，求：
（1）若在小球所在空间加一个匀强电场，发现小球水平抛出后做匀速直线运动，则电场强度E的大小和方向？
（2）若在此空间再加一个垂直纸面向外的匀强磁场，发现小球抛出后最终落地且其运动的水平位移为s，求磁感应强度B的大小？
分析：（1）小球水平抛出后做匀速直线运动，电场力与重力平衡，根据场强的定义求解场强；
（2）电场力与重力平衡，洛伦兹力提供向心力，结合几何关系求解半径，然后根据牛顿第二定律列式求解磁感应强度B的大小．
解答：解：（1）要使小球水平抛出后做匀速直线运动，小球所受合力应该为零，所以所加匀强电场方向竖直向上，大小设为E，根据平衡条件，有：
mg=Eq
可得：
E=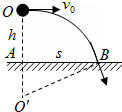
（2）由题意可得，再加一个匀强磁场后，小球在复合场中（重力场、电场、磁场）做匀速圆周运动．运动轨迹如图所示，由O运动到B．
由已知条件可知，OA间高度为h，AB间距离为s．
分别做抛出速度和落地速度方向的垂线，相交于O'点，即为小球做圆周运动的圆心，设小球做圆周运动的半径为R．
在△ABO'中，可得：R
2=s
2+（R-h）
2解得：
R= ①
由于小球做圆周运动的向心力由洛伦兹力来提供，所以：
m=qv0B可得：
R= ②
由①②两式可得：
B=答：（1）电场强度E的大小为
，方向竖直向上；（2）磁感应强度B的大小为
．
点评：本题关键明确小球的运动性质，然后根据平抛运动的分运动公式、直线运动的条件、牛顿第二定律列方程，不难．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
（2008?镇江模拟）一个质量为m带电量为+q的小球以水平初速度v0自离地面h高度处做平抛运动．不计空气阻力．重力加速度为g．试回答下列问题：
（2009?石景山区二模）如图所示，在粗糙、绝缘且足够大的水平面上固定着一个带负电的点电荷Q，将一个质量为m带电量为q的小金属块（可视为质点）放在水平面上并由静止释放，金属块将在水平面上沿远离Q的方向开始运动，设水平面足够大，则在金属块运动的整个过程中有（ ）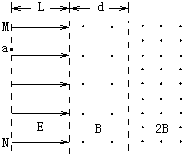
如图所示，水平方向的匀强电场的场强为E，电场区宽度为L，竖直方向足够长，紧挨着电场的是垂直纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B．一个质量为m、电量为q的带正电的粒子（不计重力）从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过tB=πm/4qB 时间穿过中间磁场，进入右边磁场，然后按某一路径再返回到电场的边界MN上的某一点b（虚线为场区的分界面），求：
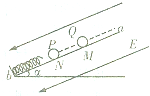如图所示，倾角为a的光滑斜面下端固定一绝缘轻弹簧，M点固定一个质量为m、带电量为-q的小球Q，整个装置处在电场强度大小为E、方向沿斜面向下的匀强电场中．现把一个带电量为+q的小球P从N点由静止释放，释放后P沿着斜面向下运动，N点与弹簧的上端和M的距离均为s0，P、Q以及弹簧的轴线ab与斜面平行，两小球均可视为质点和点电荷，弹簧的劲度系数为k0，静电力常量为k．则（ ）