
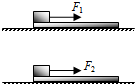
 如图,在光滑水平面上,放着两块长度相同,质量分别为M1和M2的木板,在两木板的左端各放一个大小、形状、质量完全相同的物块.开始时,各物均静止,今在两物体上各作用一水平恒力F1、F2,当物块和木板分离时,两木板的速度分别为v1和v2,物体和木板间的动摩擦因数相同,下列说法正确的是
如图,在光滑水平面上,放着两块长度相同,质量分别为M1和M2的木板,在两木板的左端各放一个大小、形状、质量完全相同的物块.开始时,各物均静止,今在两物体上各作用一水平恒力F1、F2,当物块和木板分离时,两木板的速度分别为v1和v2,物体和木板间的动摩擦因数相同,下列说法正确的是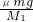 ,a2=
,a2= ,其中m为物块的质量.
,其中m为物块的质量. at12-
at12- a1t12
a1t12 at22-
at22- a2t22
a2t22 aat12-
aat12- at12
at12 abt22-
abt22- at22
at22

科目:高中物理 来源: 题型:
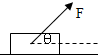 如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )
如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
查看答案和解析>>
科目:高中物理 来源: 题型:
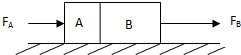 如图,在光滑水平面上放着紧靠在一起的A、B两物体,B的质量是A的2倍,B受到向右的恒力FB=2N,A受到的水平力FA=(9-2t)N(t的单位是s),从t=0开始计时,则下列说法不正确的是( )
如图,在光滑水平面上放着紧靠在一起的A、B两物体,B的质量是A的2倍,B受到向右的恒力FB=2N,A受到的水平力FA=(9-2t)N(t的单位是s),从t=0开始计时,则下列说法不正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图,在光滑水平面上,有一竖直向下的匀强磁场,分布在宽度为L的区域内,现有一边长为l(l<L)的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场,然后线圈滑出磁场的速度为v2,设线框滑进磁场的时间为t1,安接力的冲量为I1,线框产生的热量为Q1,线框滑出磁场的时间为t2,安培力的冲量为I2,线框产生的热量为Q2,则有( )
如图,在光滑水平面上,有一竖直向下的匀强磁场,分布在宽度为L的区域内,现有一边长为l(l<L)的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场,然后线圈滑出磁场的速度为v2,设线框滑进磁场的时间为t1,安接力的冲量为I1,线框产生的热量为Q1,线框滑出磁场的时间为t2,安培力的冲量为I2,线框产生的热量为Q2,则有( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com