
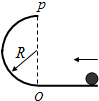
 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法不正确的是
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法不正确的是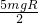
 圆弧截去,其他条件不变,则小球能达到的最大高度比P点高0.5R
圆弧截去,其他条件不变,则小球能达到的最大高度比P点高0.5R 圆弧截去,其他条件不变时小球能达到的最大高度.
圆弧截去,其他条件不变时小球能达到的最大高度.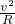 ,v=
,v=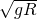

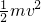 =
=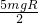 .故B正确.
.故B正确. 圆弧截去,其他条件不变,设小球能达到的最大高度为比P点高h.
圆弧截去,其他条件不变,设小球能达到的最大高度为比P点高h.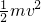 =mgh,h=
=mgh,h= =0.5R 故D正确.
=0.5R 故D正确.

科目:高中物理 来源: 题型:
 (2011?船营区模拟)如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
(2011?船营区模拟)如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.则小球落地点到O点的水平距离为
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.则小球落地点到O点的水平距离为| 5gR |
| 5gR |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com