
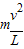 得
得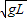 =
=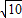 m/s
m/s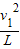
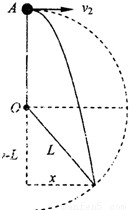
 gt2
gt2 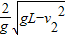 =0.6s.
=0.6s.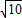 m/s 的水平速度;
m/s 的水平速度;

科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
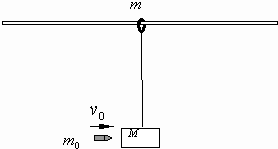 在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环.一根长为L=1m的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射穿木块,子弹穿出木块后的速度为u=200m/s (不计空气阻力和子弹与木块作用的时间),试问:
在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环.一根长为L=1m的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射穿木块,子弹穿出木块后的速度为u=200m/s (不计空气阻力和子弹与木块作用的时间),试问:查看答案和解析>>
科目:高中物理 来源: 题型:
 在足够长的光滑固定水平杆上,套有一个质量为m=0.5kg的光滑圆环.一根长为L=lm的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射入木块,子弹穿出木块时的速度为u=200m/s,子弹与木块作用的时间极短,取g=10m/s2.求:当子弹射穿木块后,木块向右摆动的最大高度h.
在足够长的光滑固定水平杆上,套有一个质量为m=0.5kg的光滑圆环.一根长为L=lm的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射入木块,子弹穿出木块时的速度为u=200m/s,子弹与木块作用的时间极短,取g=10m/s2.求:当子弹射穿木块后,木块向右摆动的最大高度h.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com