
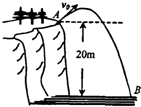
 如图所示,将一石子从20m高的山崖上斜向上抛出,抛出时速度的大小v0=15m/s,不计空气阻力,取g=10m/s2,试计算:
如图所示,将一石子从20m高的山崖上斜向上抛出,抛出时速度的大小v0=15m/s,不计空气阻力,取g=10m/s2,试计算:| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
|
| 152+2×10×20 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| ||||
| 2g |
| 152-132 |
| 2×10 |


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com