
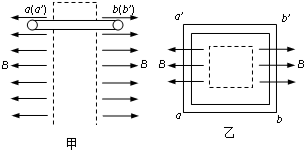
 如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.现将金属方框水平地放在磁场中,aa′边、bb′边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.金属方框由静止开始下落,其平面在下落过程中保持水平(不计空气阻力).
如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.现将金属方框水平地放在磁场中,aa′边、bb′边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.金属方框由静止开始下落,其平面在下落过程中保持水平(不计空气阻力).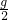 时,求方框内感应电流的功率P;
时,求方框内感应电流的功率P;

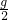 时,
时,

 mvt2+I02Rt
mvt2+I02Rt 
 .
. 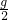 时,方框内感应电流的功率P为
时,方框内感应电流的功率P为 ;
; .
. 、F=BIL求得安培力F,根据平衡条件就能求出最大速度;
、F=BIL求得安培力F,根据平衡条件就能求出最大速度;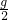 时,根据牛顿第二定律和安培力公式结合求得线框中的感应电流大小,由P=I2R求解感应电流的功率;
时,根据牛顿第二定律和安培力公式结合求得线框中的感应电流大小,由P=I2R求解感应电流的功率;

 口算能手系列答案
口算能手系列答案科目:高中物理 来源: 题型:
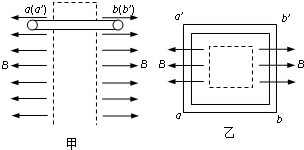 如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.现将金属方框水平地放在磁场中,aa′边、bb′边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.金属方框由静止开始下落,其平面在下落过程中保持水平(不计空气阻力).
如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.现将金属方框水平地放在磁场中,aa′边、bb′边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.金属方框由静止开始下落,其平面在下落过程中保持水平(不计空气阻力).| g | 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 (2010?杭州二模)如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.金属方框水平放置于距磁场上边界H处,由静止开始下落,其平面在下落过程中始终保持水平,当其落人磁场后,aa′整边、bb′整边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.(不计空气阻力).
(2010?杭州二模)如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.金属方框水平放置于距磁场上边界H处,由静止开始下落,其平面在下落过程中始终保持水平,当其落人磁场后,aa′整边、bb′整边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.(不计空气阻力).查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
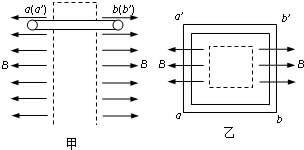
| g |
| 2 |
查看答案和解析>>
科目:高中物理 来源:2006-2007学年上海市卢湾区高三(上)期末物理试卷(解析版) 题型:解答题
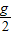 时,求方框内感应电流的功率P;
时,求方框内感应电流的功率P;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com