
 N=8N.
N=8N. .故A、B正确,C、D错误.
.故A、B正确,C、D错误.

 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
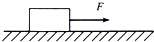 如图所示,一个质量为2kg的物体静止在光滑水平面上.现沿水平方向对物体施加10N的拉力,g取10m/s2,求:
如图所示,一个质量为2kg的物体静止在光滑水平面上.现沿水平方向对物体施加10N的拉力,g取10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量为2kg的物体与弹簧相连,弹簧的另一端固定在水平面上,物体原来处于静止状态.现用竖直向上的拉力F作用在物体上,使物体开始向上做匀加速直线运动,经0.4s弹簧刚好恢复到原长,此时物体的速度大小为2m/s,设整个过程弹簧始终在弹性限度内,取g=10m/s2.则( )
如图所示,质量为2kg的物体与弹簧相连,弹簧的另一端固定在水平面上,物体原来处于静止状态.现用竖直向上的拉力F作用在物体上,使物体开始向上做匀加速直线运动,经0.4s弹簧刚好恢复到原长,此时物体的速度大小为2m/s,设整个过程弹簧始终在弹性限度内,取g=10m/s2.则( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com