一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车做匀速直线运动.司机发现其正要通过正前方高山悬崖下的隧道,于是鸣笛,经时间t1后听到回声;听到回声再行驶△t时间后,司机第二次鸣笛,又经时间t2 后,听到回声.已知声音在空中的传播速度为v0.
(1)请根据以上条件推导客车速度的表达式.
(2)若此高速公路的最高限速为vm=120km/h,声音在空中的传播速度为v0=340m/s,测得t1=6.6s,t2=3.4s,△t=12s,请判断此客车是否超速.
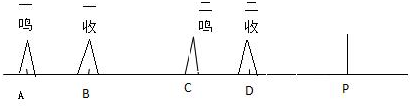
解:(1)依题可画出如图的运动示意图,由图可知
声波在时间t
1内路程为
X
AP+X
BP=v
0t
1 而车在时间t
1内路程为 X
AB=vt
1声波在时间t
2内路程为 X
CP+X
DP=v
0t
2 而车在时间t
1内路程为 X
CD=vt
2又车在△t内从B运动到C的过程有 X
BC=v△t
由几何关系得:X
BC=X
BP-X
CP X
AP+X
BP=X
AB+2X
BP X
cP+X
DP=2X
CP-X
CD联立得 v=
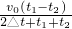
(2)带入数值可求得 V=32m/s=115.2km/h<120km/h
所以客车没有超速.
答:(1)客车速度的表达式为 v=
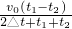
(2)客车没有超速.?
分析:(1)根据题意可以求出声波前后两次从汽车到隧道所用的时间,结合声速,进而可以求出前后两次汽车到隧道之间的距离.由于汽车向着隧道方向运动,所以两者之间的距离在减小.汽车前后两次到隧道之间的距离之差即为汽车前进的路程.由于两次声波发出的时间间隔为△t.汽车运动的时间为从第一次与声波相遇开始,到第二次与声波相遇结束.求出这个时间,就是汽车运动的时间.根据汽车运动的距离和时间,即可求出汽车的运动速度表达式;
(2)此高速公路的最高限速为v
m=120km/h,声音在空中的传播速度为v
0=340m/s,测得t
1=6.6s,t
2=3.4s,△t=12s,将此代入第(1)可判定是否超速.
点评:如何确定汽车运动的时间,是此题的难点.两次信号的时间间隔虽然是12秒,但汽车在接收到两次信号时其通过的路程所对应的时间不是12秒.要从起第一次接收到超声波的信号开始计时,到第二次接收到超声波的信号结束,由此来确定其运动时间.通过的路程与通过这段路程所用的时间对应上是解决此题关键.

 解:(1)依题可画出如图的运动示意图,由图可知
解:(1)依题可画出如图的运动示意图,由图可知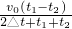
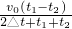


 阅读快车系列答案
阅读快车系列答案 一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车保持速度不变.司机发现其正要通过正前方高山悬崖下的隧道,于是鸣笛,5s后听到回声;听到回声后又行驶10s司机第二次鸣笛,3s后听到回声.请根据以上数据帮助司机计算一下客车的速度,看客车是否超速行驶.已知此高速公路的最高限速为110km/h(如图所示),声音在空中的传播速度为340m/s.
一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车保持速度不变.司机发现其正要通过正前方高山悬崖下的隧道,于是鸣笛,5s后听到回声;听到回声后又行驶10s司机第二次鸣笛,3s后听到回声.请根据以上数据帮助司机计算一下客车的速度,看客车是否超速行驶.已知此高速公路的最高限速为110km/h(如图所示),声音在空中的传播速度为340m/s.