
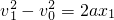 ⑤
⑤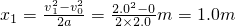 ⑥
⑥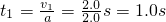
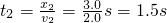 ⑨
⑨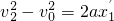
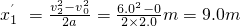
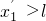 ,所以小物体由A到B一直做匀加速直线运动,设小物体由A到B的时间为t',则有
,所以小物体由A到B一直做匀加速直线运动,设小物体由A到B的时间为t',则有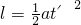
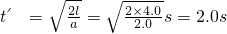


科目:高中物理 来源: 题型:
 如图所示,水平放置的平行金属板A、B间距为d,带电粒子的电荷量为q,质量为m,粒子以速度v从两极板中央处水平飞入两极板间,当两板上不加电压时,粒子恰从下板的边缘飞出.现给AB加上一电压,则粒子恰好从上极板边缘飞出求:(1)两极板间所加电压U;(2)金属板的长度L.
如图所示,水平放置的平行金属板A、B间距为d,带电粒子的电荷量为q,质量为m,粒子以速度v从两极板中央处水平飞入两极板间,当两板上不加电压时,粒子恰从下板的边缘飞出.现给AB加上一电压,则粒子恰好从上极板边缘飞出求:(1)两极板间所加电压U;(2)金属板的长度L.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,水平放置的矩形线圈abcd的面积为S,处于竖直向下的磁感应强度为B的匀强磁场内,则穿过矩形线圈的磁通量是
如图所示,水平放置的矩形线圈abcd的面积为S,处于竖直向下的磁感应强度为B的匀强磁场内,则穿过矩形线圈的磁通量是查看答案和解析>>
科目:高中物理 来源: 题型:
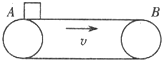 如图所示,水平放置的白色的传送带以速度v=6m/s向右匀速运行,现将一小煤块轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.1,若A端与B端相距30m,则(g=10m/s2)( )
如图所示,水平放置的白色的传送带以速度v=6m/s向右匀速运行,现将一小煤块轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.1,若A端与B端相距30m,则(g=10m/s2)( )| A、小煤块先作匀加速直线运动,后作匀速直线运动 | B、小煤块一直作匀加速直线运动 | C、全过程中,小煤块先受到向右的滑动摩擦力,后不受摩擦力作用 | D、全过程中,小煤块先受到向右的滑动摩擦力,后受到向右的静摩擦力作用 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,水平放置的两块长直平行金属板a、b相距d=0.10m,a、b间的电场强度为E=5.0×105N/C,b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10?18C的带正电的粒子(不计重力),从贴近a板的左端以υ0=1.0×106m/s的初速度水平射入匀强电场,刚好从狭缝P穿过b板而垂直进入匀强磁场,最后粒子回到边界b的Q(图中未标出)处.试求
如图所示,水平放置的两块长直平行金属板a、b相距d=0.10m,a、b间的电场强度为E=5.0×105N/C,b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10?18C的带正电的粒子(不计重力),从贴近a板的左端以υ0=1.0×106m/s的初速度水平射入匀强电场,刚好从狭缝P穿过b板而垂直进入匀强磁场,最后粒子回到边界b的Q(图中未标出)处.试求查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,水平放置的平行板电容器,原来AB两板不带电,B极板接地,它的极板长L=0.1m,两板间距离d=0.4×10-2m,现有一微粒质量m=2.0×10-6kg,带电量q=+1.0×10-8C,以一定初速度从两板中央平行于极板射入,由于重力作用微粒恰好能落到A板上中点O处,不反弹.忽略平行板电容器的边缘效应,取g=10m/s2.试求:
如图所示,水平放置的平行板电容器,原来AB两板不带电,B极板接地,它的极板长L=0.1m,两板间距离d=0.4×10-2m,现有一微粒质量m=2.0×10-6kg,带电量q=+1.0×10-8C,以一定初速度从两板中央平行于极板射入,由于重力作用微粒恰好能落到A板上中点O处,不反弹.忽略平行板电容器的边缘效应,取g=10m/s2.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com