
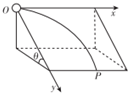
 �ʵ���v0������ԭ��O��Ox�����׳����ع⻬б���˶�����ص�ΪP��������������ͼ��ʾ���ı�⻬б�����ǣ�ʹ�ȷֱ�Ϊ30�㡢45�㡢60�㣬��б��߶�ʼ�ղ��䣬ˮƽ���ٶ�v0���䣮���������龰�����ʱ�ʵ��˶���ˮƽλ�Ʒֱ�Ϊx1��x2��x3���ʵ��˶���ʱ��t1��t2��t3�������ж���ȷ���ǣ�������
�ʵ���v0������ԭ��O��Ox�����׳����ع⻬б���˶�����ص�ΪP��������������ͼ��ʾ���ı�⻬б�����ǣ�ʹ�ȷֱ�Ϊ30�㡢45�㡢60�㣬��б��߶�ʼ�ղ��䣬ˮƽ���ٶ�v0���䣮���������龰�����ʱ�ʵ��˶���ˮƽλ�Ʒֱ�Ϊx1��x2��x3���ʵ��˶���ʱ��t1��t2��t3�������ж���ȷ���ǣ�������| A�� | t1��t2��t3 | B�� | x1��x2��x3 | ||
| C�� | ���ʱ�ʵ���ٶ���x��н���ͬ | D�� | ���ʱ�ʵ������Ĺ�����ͬ |
���� ���ʵ���˶��ֽ�Ϊˮƽ�������б�����·�������б�淽���λ�Ƶó��˶���ʱ�䣬�Ӷ��Ƚ�ʱ��ij��̣�ץס���ٶ���ͬ���Ƚ�ˮƽλ�ƵĴ�С�������ٶ�λ�ƹ�ʽ�ó����ʱ��y������ٶ���ͬ�����ƽ���ı��ζ���Ƚ���ص��ٶȷ�����x��ļнǣ�����������˲ʱ���ʹ�ʽ�Ƚ������Ĺ��ʴ�С��
��� �⣺���ʵ����б��ĸ߶�Ϊh�����ʵ��ڹ⻬б���ϵļ��ٶ�a=gsin�ȣ����ʱ��y����˶�λ��Ϊy=$\frac{h}{sin��}$����y=$\frac{1}{2}a{t}^{2}$��֪��$t=\frac{1}{sin��}\sqrt{\frac{2h}{g}}$�������t1��t2��t3
����A��ȷ��
���ڳ��ٶ�v0���䣬��x=v0t��֪��x1��x2��x3����B��ȷ��
��${{v}_{y}}^{2}=2ay=2gh$֪�����ʱ�ʵ���y���������ͬ��������ʱ�ʵ���ٶ���x��н���ͬ����C��ȷ��
��P=mgvysin�ȿ�֪�����ʱ�����Ĺ��ʲ�ͬ����D����
��ѡ��ABC��
���� �������Ĺؼ����մ��������˶��ķ�����֪���ʵ���x�����y�����ϵ��˶����ɣ�ץס��ʱ�ԣ�����˶�ѧ��ʽ�����⣮


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 1.0Wb | B�� | 0.5��10-2Wb | C�� | 0.5��10-1Wb | D�� | 1.0��10-2Wb |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | A�ӵ�ѹ��V1�ġ�+����������B�ӵ�ѹ��V1�ġ�-����������C�ӵ�ѹ��V2�ġ�+����������D�ӵ�ѹ��V2�ġ�-�������� | |
| B�� | �����������Ļ���ͷ�����ƶ�ʱ��ѹ��V1��ʾ����С����ѹ��V2��ʾ������ | |
| C�� | �����������Ļ���ͷ�����ƶ�ʱ��ѹ��V1��ʾ������ѹ��V2��ʾ����С | |
| D�� | ���ۻ����������Ļ���ͷ�����ƶ����������ƶ�����ѹ��V1��V2��ʾ��֮�Ͳ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��12����ͬ��ľ�����ˮƽ�������ų�һ��ֱ�ߣ�������ľ��Ӵ�����ճ����ÿ��ľ�������m=1.2kg������l=0.5m��ľ��ԭ������ֹ������������Ķ�Ħ��������Ϊ��1=0.1������ߵ�һ��ľ�����˷�һ����M=1kg��СǦ�飨����Ϊ�ʵ㣩�������ľ���Ķ�Ħ������Ϊ��2=0.5����ͻȻ��Ǧ��һ�����ҵij��ٶ�v0=9m/s��ʹ����ľ���ϻ��У���ľ�������估Ǧ����ľ�������Ħ���������ڻ����Ӳ������������ٶ�g=10m/s2����
��ͼ��ʾ��12����ͬ��ľ�����ˮƽ�������ų�һ��ֱ�ߣ�������ľ��Ӵ�����ճ����ÿ��ľ�������m=1.2kg������l=0.5m��ľ��ԭ������ֹ������������Ķ�Ħ��������Ϊ��1=0.1������ߵ�һ��ľ�����˷�һ����M=1kg��СǦ�飨����Ϊ�ʵ㣩�������ľ���Ķ�Ħ������Ϊ��2=0.5����ͻȻ��Ǧ��һ�����ҵij��ٶ�v0=9m/s��ʹ����ľ���ϻ��У���ľ�������估Ǧ����ľ�������Ħ���������ڻ����Ӳ������������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | F | B�� | 2F | C�� | 4F | D�� | $\frac{F}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
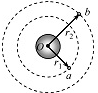 ��ͼ��ʾ����������������a��b���Ƶ���������Բ���˶���a��b������O�ľ���ֱ�Ϊr1��r2�����ٶȴ�С�ֱ�Ϊv1��v2�����ٶȴ�С�ֱ�Ϊ��1����2�����ļ��ٶȴ�С�ֱ�Ϊa1��a2�����ڴ�С�ֱ�ΪT1��T2������˵����ȷ���ǣ�������
��ͼ��ʾ����������������a��b���Ƶ���������Բ���˶���a��b������O�ľ���ֱ�Ϊr1��r2�����ٶȴ�С�ֱ�Ϊv1��v2�����ٶȴ�С�ֱ�Ϊ��1����2�����ļ��ٶȴ�С�ֱ�Ϊa1��a2�����ڴ�С�ֱ�ΪT1��T2������˵����ȷ���ǣ�������| A�� | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | B�� | $\frac{{��}_{1}}{{��}_{2}}$=$\sqrt{��\frac{{r}_{2}}{{r}_{1}}��^{3}}$ | C�� | $\frac{{a}_{1}}{{a}_{2}}$=��$\frac{{r}_{2}}{{r}_{1}}$��3 | D�� | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{��\frac{{r}_{1}}{{r}_{2}}��}$3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
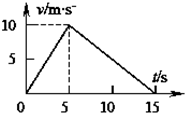 ����Ϊ3kg�����徲ֹ��ˮƽ�����ϣ�����ˮƽ��F����5s��ȥ�������˶����ٶ�ͼ����ͼ����
����Ϊ3kg�����徲ֹ��ˮƽ�����ϣ�����ˮƽ��F����5s��ȥ�������˶����ٶ�ͼ����ͼ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 10m | B�� | 20m | C�� | 30m | D�� | 40m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
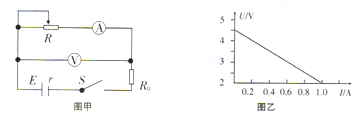
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com