
 如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1.6kg的无人机,其动力系统所能提供的最大升力F=36N,已知每个旋翼所能提供的升力Fi=kωi2,(k为常数,ωi为旋翼转动的角速度),运动过程中所受空气阻力大小恒为f=4N,取g=10m/s2.
如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1.6kg的无人机,其动力系统所能提供的最大升力F=36N,已知每个旋翼所能提供的升力Fi=kωi2,(k为常数,ωi为旋翼转动的角速度),运动过程中所受空气阻力大小恒为f=4N,取g=10m/s2.分析 (1)根据牛顿第二定律求出以最大升力竖直向上起飞的加速度,结合位移时间公式求出5s时离地的高度.
(2)抓住最大升力与旋翼角速度的关系求出最大角速度,抓住悬停时重力等于升力,求出旋翼的角速度,从而得出旋翼转动的角速度与提供最大升力时旋翼的角速度之比.
(3)根据牛顿第二定律求出下落的加速度,以及恢复最大升力后的加速度,抓住位移关系求出最大速度,从而结合速度时间公式求出无人机从开始下落到恢复升力的最长时间.
解答 解:(1)由牛顿第二定律得:F-mg-f=ma,
代入数据解得:a=10m/s2,
上升高度:h=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×10×25m=125m$.
(2)动力系统所能提供的最大升力时:36=$4k{{ω}_{m}}^{2}$
即:$k{{ω}_{m}}^{2}=9$,
悬停在H=90m处时:$4k{{ω}_{i}}^{2}=mg$
即:$k{{ω}_{i}}^{2}=4$,
所以$\frac{{ω}_{i}}{{ω}_{m}}=\frac{2}{3}$.
(3)下落过程中:mg-f=ma1
代入数据解得:${a}_{1}=7.5m/{s}^{2}$.
恢复升力后向下减速运动过程:F-mg+f=ma2,
代入数据解得加速度大小为:${a}_{2}=15m/{s}^{2}$.
设恢复升力时的速度为vm,则有:$\frac{{{v}_{m}}^{2}}{2{a}_{1}}+\frac{{{v}_{m}}^{2}}{2{a}_{2}}=H$,
代入数据解得:vm=30m/s.
由vm=a1tm得:${t}_{m}=\frac{30}{7.5}s=4s$.
答:(1)t=5s时离地面的高度为125m;
(2)其旋翼转动的角速度与提供最大升力时旋翼的角速度之比为$\frac{2}{3}$;
(3)无人机从开始下落到恢复升力的最长时间为4s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,关键理清无人机在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,知道加速度是联系力学和运动学的桥梁.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中物理 来源: 题型:选择题
| A. | 油的密度 | B. | 油的摩尔体积 | C. | 油的摩尔质量 | D. | 油滴的质量 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体受拉力作用向上匀速运动,拉力做的功是1J,但物体重力势能的增加量不是1J | |
| B. | 物体受拉力作用向上运动,拉力做的功是1J,但物体重力势能的增加量不是1J | |
| C. | 没有摩擦时物体由A沿直线运动到B,克服重力做的功是1 J,有摩擦时物体由A沿曲线运动到B,克服重力做的功大于1 J | |
| D. | 物体运动,重力做的功是-1J,物体重力势能增加1J |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
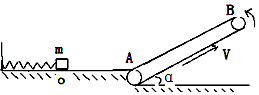 如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
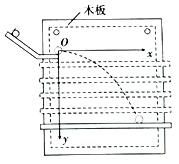 某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.
某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 卫星运行的加速度大小为$\frac{8{π}^{2}R}{{T}^{2}}$ | |
| B. | 该星球的第一宇宙速度大小为$\frac{2πR}{T}$ | |
| C. | 该星球表面的重力加速度大小为$\frac{108{π}^{2}R}{{T}^{2}}$ | |
| D. | 该星球的密度为$\frac{81π}{GT}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | F=G$\frac{Mm}{r}$ | B. | F=G$\frac{Mm}{{r}^{2}}$ | C. | F=G$\frac{Mm}{R}$ | D. | F=G$\frac{Mm}{{R}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com