
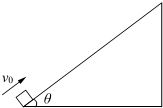
 一个倾角为θ=37°的斜面固定在水平面上,一个质量为m=1.0kg的小物块(可视为质点)以v0=4.0m/s的初速度由底端沿斜面上滑,小物块与斜面的动摩擦因数μ=0.25.若斜面足够长,已知sin37°=0.6,cos37°=0.8,g取10m/s2,求:
一个倾角为θ=37°的斜面固定在水平面上,一个质量为m=1.0kg的小物块(可视为质点)以v0=4.0m/s的初速度由底端沿斜面上滑,小物块与斜面的动摩擦因数μ=0.25.若斜面足够长,已知sin37°=0.6,cos37°=0.8,g取10m/s2,求:
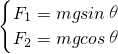
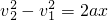 ⑤
⑤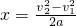 =
=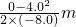 =1.0m⑥
=1.0m⑥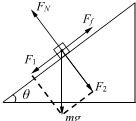
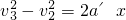 ⑩
⑩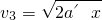 =
=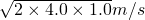 =
=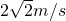 (或2.8m/s)
(或2.8m/s)  m/s.
m/s.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中物理 来源: 题型:
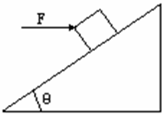 一个倾角为37°的斜面固定不动,其上有一个重10N的物体静止不动,当给物体加一个水平向右的从零逐渐增大到8N的推力作用时物体仍不动下列说法正确的是( )
一个倾角为37°的斜面固定不动,其上有一个重10N的物体静止不动,当给物体加一个水平向右的从零逐渐增大到8N的推力作用时物体仍不动下列说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
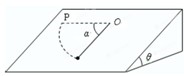 如图所示,在一个倾角为θ=37°(cos37°=0.8)的斜面上,O点固定一根细绳,细绳另一端连接一个质点.现将质点放到斜面上P点,由静止释放,已知OP连线水平且间距为绳长,质点滑动到细绳转过角度α=90°的位置时刚好停止.问:
如图所示,在一个倾角为θ=37°(cos37°=0.8)的斜面上,O点固定一根细绳,细绳另一端连接一个质点.现将质点放到斜面上P点,由静止释放,已知OP连线水平且间距为绳长,质点滑动到细绳转过角度α=90°的位置时刚好停止.问:查看答案和解析>>
科目:高中物理 来源: 题型:
 有一个倾角为37°的固定斜面,斜面长l=3.2m,现将一个质量m=1.0kg的物体放在斜面顶端,对物体施加一个沿斜面向上的恒力F作用F=2.4N.物体从静止开始沿斜面匀加速下滑,经过时间2s,物体恰好滑至斜面底端.
有一个倾角为37°的固定斜面,斜面长l=3.2m,现将一个质量m=1.0kg的物体放在斜面顶端,对物体施加一个沿斜面向上的恒力F作用F=2.4N.物体从静止开始沿斜面匀加速下滑,经过时间2s,物体恰好滑至斜面底端.查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com