
 质量均为m的两小球A、B间有压缩的轻、短弹簧,弹簧处于锁定状态,两球的大小尺寸和弹簧尺寸都可忽略,把它们放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,B球仍然保持静止,A球能上升的最大高度为R,如图(甲)所示.现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R 的固定半圆槽左端的M 点由静止开始滑下,如图(乙)所示,到达半圆槽的最低点时解除弹簧锁定,求A 球离开半圆槽后能上升的最大高度.
质量均为m的两小球A、B间有压缩的轻、短弹簧,弹簧处于锁定状态,两球的大小尺寸和弹簧尺寸都可忽略,把它们放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,B球仍然保持静止,A球能上升的最大高度为R,如图(甲)所示.现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R 的固定半圆槽左端的M 点由静止开始滑下,如图(乙)所示,到达半圆槽的最低点时解除弹簧锁定,求A 球离开半圆槽后能上升的最大高度.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2gR |
| gR |
| 2gR |
| gR |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中物理 来源: 题型:
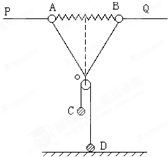 如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量?
如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量?查看答案和解析>>
科目:高中物理 来源: 题型:
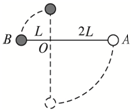 如图所示,质量均为m的两小球A和B用长为3L的轻杆相连,轻杆可绕距A小球2L的轴O在竖直平面内自由转动.现将轻杆拉至水平位置并由静止释放,试求:
如图所示,质量均为m的两小球A和B用长为3L的轻杆相连,轻杆可绕距A小球2L的轴O在竖直平面内自由转动.现将轻杆拉至水平位置并由静止释放,试求:查看答案和解析>>
科目:高中物理 来源: 题型:
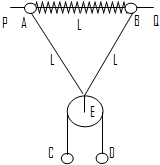 如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)
如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)查看答案和解析>>
科目:高中物理 来源: 题型:
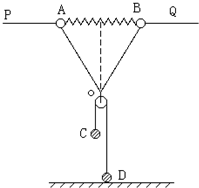 如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.,O的下端为质量不计的光滑定滑轮,质量为m/2的C球用轻绳跨过定滑轮与置于水平地面上质量为2m的D球相连,求弹簧的原长?
如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.,O的下端为质量不计的光滑定滑轮,质量为m/2的C球用轻绳跨过定滑轮与置于水平地面上质量为2m的D球相连,求弹簧的原长?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com