
分析 根据万有引力等于重力求出地球的质量,根据万有引力提供向心力求出飞船的轨道半径,结合万有引力等于重力求出飞船处的重力加速度.
解答 解:物体m0在地球表面 m0g=$\frac{GM{m}_{0}}{{R}^{2}}$
解得地球质量 M=$\frac{g{R}^{2}}{G}$
飞船(质量为m)在轨道上运行:$\frac{GMm}{{r}^{2}}=mr(\frac{2π}{T})^{2}$
而 mg′=$\frac{GMm}{{r}^{2}}$
联立以上得g′=$\frac{(4{π}^{2})^{\frac{2}{3}}{g}^{\frac{1}{3}}{R}^{\frac{2}{3}}}{{T}^{\frac{4}{3}}}$.
答:地球的质量M为$\frac{g{R}^{2}}{G}$,飞船所在处的重力加速度为$\frac{{(4{π}^{2})}^{\frac{2}{3}}{g}^{\frac{1}{3}}{R}^{\frac{2}{3}}}{{T}^{\frac{4}{3}}}$.
点评 解决本题的关键掌握万有引力等于重力和万有引力提供向心力两个理论,并能灵活运用.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
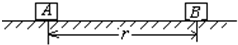 如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:
如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
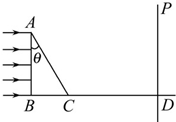 如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏,现一宽度等于AB的单色平行光束垂直射向AB面,在屏P上形成一条宽度等于$\frac{2}{3}\overline{AB}$的光带,求棱镜的折射率.
如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏,现一宽度等于AB的单色平行光束垂直射向AB面,在屏P上形成一条宽度等于$\frac{2}{3}\overline{AB}$的光带,求棱镜的折射率.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
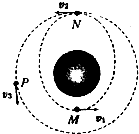 如图所示,发射某飞船时,先将飞船发送到一个椭圆轨道上,其近地点M距地面200km,远地点N距地面330km.进入该轨道正常运行时,其周期为T1,通过M、N点时的速率分别是v1,v2,加速度分别为a1,a2.当飞船某次通过N点时,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面330km的圆形轨道,开始绕地球做匀速圆周运动,周期为T2,这时飞船的速率为v3,加速度为a3.比较飞船在M、N、P三点正常运行时(不包括点火加速阶段)的速率大小和加速度大小及在两个轨道上运行的周期,下列结论不正确的是( )
如图所示,发射某飞船时,先将飞船发送到一个椭圆轨道上,其近地点M距地面200km,远地点N距地面330km.进入该轨道正常运行时,其周期为T1,通过M、N点时的速率分别是v1,v2,加速度分别为a1,a2.当飞船某次通过N点时,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面330km的圆形轨道,开始绕地球做匀速圆周运动,周期为T2,这时飞船的速率为v3,加速度为a3.比较飞船在M、N、P三点正常运行时(不包括点火加速阶段)的速率大小和加速度大小及在两个轨道上运行的周期,下列结论不正确的是( )| A. | v1>v3 | B. | v1>v2 | C. | a2=a3 | D. | T1>T2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
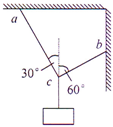 用三根轻绳将质量为m的物块悬挂在空中,如图所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )
用三根轻绳将质量为m的物块悬挂在空中,如图所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )| A. | $\frac{\sqrt{3}}{2}$mg $\frac{1}{2}$mg | B. | $\frac{1}{2}$mg $\frac{\sqrt{3}}{2}$mg | C. | $\frac{\sqrt{3}}{4}$mg $\frac{1}{2}$mg | D. | $\frac{1}{2}$mg $\frac{\sqrt{3}}{4}$mg |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
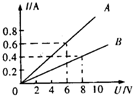 如图为A、B两个电阻的电压-电流图象,根据图象可得到:RA=10Ω,RB=20Ω;若将两个电阻分别接入电路时,两电阻两端电压之比为16:5,则通过它们的电流之比为32:5.
如图为A、B两个电阻的电压-电流图象,根据图象可得到:RA=10Ω,RB=20Ω;若将两个电阻分别接入电路时,两电阻两端电压之比为16:5,则通过它们的电流之比为32:5.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
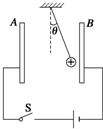 如图所示,平行板电容器的两极板A、B接在电池的两极,一带正电的小球悬挂在电容器内部,闭合开关S,给电容器充电,稳定后悬线偏离竖直方向的夹角为θ,则( )
如图所示,平行板电容器的两极板A、B接在电池的两极,一带正电的小球悬挂在电容器内部,闭合开关S,给电容器充电,稳定后悬线偏离竖直方向的夹角为θ,则( )| A. | 若保持开关S闭合,A极板向B极板靠近,则θ增大 | |
| B. | 若保持开关S闭合,A极板向B极板靠近,则θ不变 | |
| C. | 若开关S断开,A极板向B极板靠近,则θ不变 | |
| D. | 若开关S断开,A极板向B极板靠近,则θ增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com