
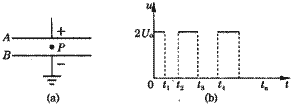
 ��2002?���ϣ���ͼ��a����ʾ��A��BΪˮƽ���õ�ƽ�н����壬������Ϊd��dԶС�ڰ�ij��Ϳ�����������֮����һ��������ʵ�P����֪����A��B��ӵ�ѹUo�����ʵ�P���Ծ�ֹƽ�⣮����A��B�������ͼ��b����ʾ����ʱ��t�仯�ĵ�ѹu����t=0ʱ�ʵ�Pλ��A��B����е㴦�ҳ���Ϊ�㣮��֪�ʵ�P����A��B֮�������ķ��������˶����ֲ���������������ͼ��b����u�ı�ĸ�ʱ��t1��t2��t3��tn�ı���ʽ�����ʵ㿪ʼ���е���������ߵ㣬���Ժ�ÿ�δ���ߵ㵽��͵�����͵㵽��ߵ�Ĺ����У���ѹֻ�ı�һ�Σ���
��2002?���ϣ���ͼ��a����ʾ��A��BΪˮƽ���õ�ƽ�н����壬������Ϊd��dԶС�ڰ�ij��Ϳ�����������֮����һ��������ʵ�P����֪����A��B��ӵ�ѹUo�����ʵ�P���Ծ�ֹƽ�⣮����A��B�������ͼ��b����ʾ����ʱ��t�仯�ĵ�ѹu����t=0ʱ�ʵ�Pλ��A��B����е㴦�ҳ���Ϊ�㣮��֪�ʵ�P����A��B֮�������ķ��������˶����ֲ���������������ͼ��b����u�ı�ĸ�ʱ��t1��t2��t3��tn�ı���ʽ�����ʵ㿪ʼ���е���������ߵ㣬���Ժ�ÿ�δ���ߵ㵽��͵�����͵㵽��ߵ�Ĺ����У���ѹֻ�ı�һ�Σ���| qU0 |
| d |
| 2qU0 |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
|
| ||
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2 |
|
| 2 |
|
| 2 |
|
| ||
| 2 |
|
| 2 |
|
| 2 |
|
| 2 |
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
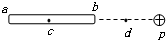 ��2002?���ϣ���ͼ��ʾ����ԭ��������Ľ���ϸ��ab����P��������һ�������ɣ��ﵽ����ƽ���������
��2002?���ϣ���ͼ��ʾ����ԭ��������Ľ���ϸ��ab����P��������һ�������ɣ��ﵽ����ƽ����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��2002?���ϣ���ͼ��������ʾ�����������ǿ�糡����ǿ�ų���ȡ������ͼ��ʾ��һ����������x�����������������ڴ���������Ĺ������˶�����ʼ�ղ�����ƫת������������Ӱ�죬�糡ǿ��E�ʹŸ�Ӧǿ��B�ķ�������ǣ�������
��2002?���ϣ���ͼ��������ʾ�����������ǿ�糡����ǿ�ų���ȡ������ͼ��ʾ��һ����������x�����������������ڴ���������Ĺ������˶�����ʼ�ղ�����ƫת������������Ӱ�죬�糡ǿ��E�ʹŸ�Ӧǿ��B�ķ�������ǣ��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
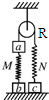 ��2002?���ϣ���ͼ��a��b��cΪ������飬M��NΪ�������ʵ��ɣ�RΪ����⻬�����ֵ�����������������ͼ��ʾ������ƽ��״̬��������
��2002?���ϣ���ͼ��a��b��cΪ������飬M��NΪ�������ʵ��ɣ�RΪ����⻬�����ֵ�����������������ͼ��ʾ������ƽ��״̬���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
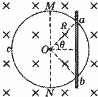 ��2002?���ϣ���ͼ��ʾ���뾶ΪR����λ���ȵ���Ϊ�˵ľ��ȵ���Բ���̶���ˮƽ���ϣ�Բ������ΪO����ǿ�ų���ֱˮƽ�淽�����£��Ÿ�ǿ��ΪB��ƽ����ֱ��MON�ĵ���ˣ��ش�ֱ�ڸ˵ķ��������˶����˵ĵ�����Ժ��Բ��ƣ�����Բ���Ӵ����ã�ijʱ�̣��˵�λ����ͼ����aOb=2�ȣ��ٶ�Ϊv�����ʱ�������ڸ��ϰ������Ĵ�С��
��2002?���ϣ���ͼ��ʾ���뾶ΪR����λ���ȵ���Ϊ�˵ľ��ȵ���Բ���̶���ˮƽ���ϣ�Բ������ΪO����ǿ�ų���ֱˮƽ�淽�����£��Ÿ�ǿ��ΪB��ƽ����ֱ��MON�ĵ���ˣ��ش�ֱ�ڸ˵ķ��������˶����˵ĵ�����Ժ��Բ��ƣ�����Բ���Ӵ����ã�ijʱ�̣��˵�λ����ͼ����aOb=2�ȣ��ٶ�Ϊv�����ʱ�������ڸ��ϰ������Ĵ�С���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com