Question

一个质点，在惯性系K′中做匀速圆周运动，轨道方程为x′²+y′²=a²，z′=0.

试证：在惯性系K中的观察者测得该质点做椭圆运动，椭圆的中心以速度v移动.

Answer 1

解析：惯性系K′系相对K做匀速直线运动，圆周轨道相对K′静止，圆心在K系的坐标原点处， K系中的观察者测得该轨道在相对运动方向上的直径将较K′中的短，在垂直于运动方向上的长度不变，此即“长度收缩”效应.

设K′、K系的对应坐标轴分别平行，K′系相对速度v沿x轴正向运动，x、x′ 轴重合，并且t=t′=0时坐标原点O、O′重合，对K′系圆周轨道上某坐标为（x′，y′）的点，O′x′是固有长度，在K系中测该段长度，由“长度收缩”效应，得

x-vt=x′

在垂直于运动方向上的长度不变，y=y′，z=z′，代入K′系的轨道方程得

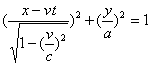
所以，在K系中测得的轨迹是椭圆，半长轴为a、半短轴为a，椭圆的中心相对O′的移动速度即参考系K相对K′的运动速度v.