
分析 据万有引力等于向心力,可以列式求解出行星的质量,进一步求出密度.
解答 解:(1)设行星质量为M,卫星质量为m,行星对卫星的万有引力提供向心力,则:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$;
(2)由于M=ρV,
所以ρ=$\frac{M}{V}$=$\frac{3{πr}^{3}}{{{GT}^{2}R}^{3}}$.
答:(1)行星的质量是$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$;
(2)若行星的半径为R,则行星密度为$\frac{3{πr}^{3}}{{{GT}^{2}R}^{3}}$.
点评 本题关键要掌握万有引力等于向心力列出等式求解.要注意轨道半径和星球半径的关系.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中物理 来源: 题型:解答题
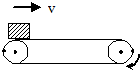 一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.
一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
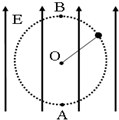 如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )
如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )| A. | 小球一定做变速圆周运动 | |
| B. | 小球可能做匀速圆周运动 | |
| C. | 小球经过最低点A时绳子拉力一定最小 | |
| D. | 小球经过最高点B时绳子拉力可能最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
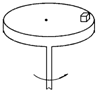 质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )
质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )| A. | 物体受重力、弹力、摩擦力和向心力作用 | |
| B. | 物体所受摩擦力在圆轨道的切线方向,与线速度方向相反 | |
| C. | 物体所受摩擦力指向圆心,提供物体运动所需的向心力 | |
| D. | 物体不受摩擦力的作用 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
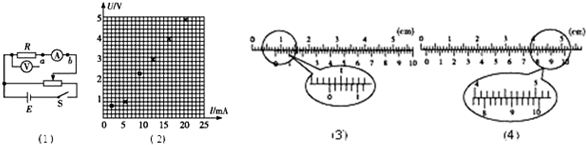
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | r1=r2 T1≠T2 | B. | r1≠r2 T1≠T2 | C. | r1=r2 T1=T2 | D. | r1≠r2 T1=T2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
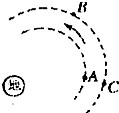 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )| A. | 线速度大小的关系是VA<VB=VC | |
| B. | 周期关系是TA>TB=TC | |
| C. | 向心力大小的关系是FA=FB<FC | |
| D. | 轨道半径和周期的关系是$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com