一列队伍长120m,行进速度v1=1.6m/s,为了传达一个命令,通讯员从队伍的排尾以速度v2=3m/s的速度跑步赶到队伍排头,然后又立即以大小为1.6m/s的速度赶回到排尾.试问:
(1)通讯员从离开队尾到重新回到队尾共需要多少时间?
(2)通讯员归队与离队处相距多远?
见解析
【试题分析】
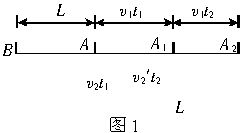
【解析】 本题两个研究对象:通讯员和行进中的队伍,两者都做匀速直线运动,其运动过程如图1所示.设队伍原位置为AB,通讯员从排尾赶到排头时,排头已到位置A
1,所用时间为t
1;通讯员返回排尾时,排头的位置为A
2,所用时间为t
2.在t
1内,通讯员与队伍的位移之差为L;在t
2时间内通讯员与队伍位移大小之和等于L.
解法一:(1)通讯员从排尾赶到排头时,有关系式
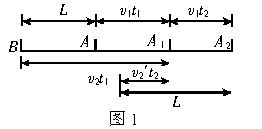
v
2t
1-v
1t
1=L
设通讯员从排头返回排尾的速度为v
2′,其大小为v
2′=v
1=1.6m/s,又有关系
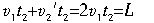
联立以上两式得,通讯员从离开队伍到重新返回排尾共需时间
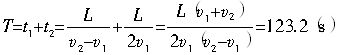
(2)通讯员归队处与离队处相距距离就是队伍前进的距离,即
s=v
1T=1.6×123.2m=197.1m
解法二:用相对法求解,既对通讯员换另一个参考系.根据运动的相对性,如果把行进中的队伍作为参考系,就可以简化为一个研究对象,即通讯员相对于“静止”的队伍做匀速直线运动.离队时,通讯员以大小等于(v
2-v
1)的速度向排头做匀速运动,赶到排头所需的时间t
1=
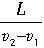
;返回时通讯员以大小等于2v
1的速度向排尾匀速运动,回到排尾所需的时间t
2=
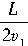
,所以可得通讯员从离队到归队的时间
T =
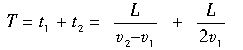
=
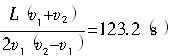
再以地面为参考系,队伍前进的距离即为通讯员离出发点的距离
s=v
1T=1.6×123.2m=197.1m


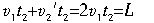
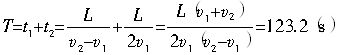
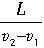 ;返回时通讯员以大小等于2v1的速度向排尾匀速运动,回到排尾所需的时间t2=
;返回时通讯员以大小等于2v1的速度向排尾匀速运动,回到排尾所需的时间t2=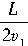 ,所以可得通讯员从离队到归队的时间
,所以可得通讯员从离队到归队的时间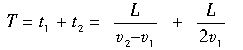
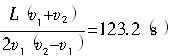


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案