
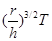 ;(2)
;(2)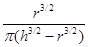 (arcsin
(arcsin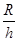 +arcsin
+arcsin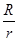 )T
)T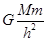 =mh
=mh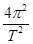 ①
①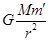 =m′r
=m′r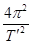 ②
②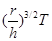 ③
③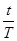 ×2π,β=
×2π,β=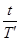 ×2π ④
×2π ④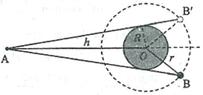
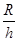 +arcsin
+arcsin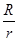 ) ⑤
) ⑤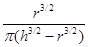 (arcsin
(arcsin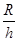 +arcsin
+arcsin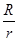 )T
)T

科目:高中物理 来源:不详 题型:单选题
| A.第一宇宙速度是能使卫星绕地球运行的最小发射速度 |
| B.第一宇宙速度是人造卫星绕地球运行的最小速度 |
| C.第二宇宙速度是卫星在椭圆轨道上运行时近地点的速度 |
| D.第三宇宙速度是发射人造地球卫星的最小速度 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 环绕该行星做匀速圆周运动的卫星,已知卫星质量为
环绕该行星做匀速圆周运动的卫星,已知卫星质量为 ,该行星的半径是卫星运动轨道半径的
,该行星的半径是卫星运动轨道半径的 .求:
.求:查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
 的卫星绕地球做匀速圆周运动,运动的轨道半径之比
的卫星绕地球做匀速圆周运动,运动的轨道半径之比 ,则下列关于两颗卫星的说法中正确的是
,则下列关于两颗卫星的说法中正确的是A.线速度大小之比为 |
B.向心加速度大小之比为 |
C.运动的周期之比为 |
D.动能之比为 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
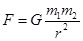 ,下列说法正确的是( )
,下列说法正确的是( )| A.公式中的G是引力常量,它是人为规定的 |
| B.当两物体间的距离r趋于零时,万有引力趋于无穷大 |
| C.两物体间的引力大小一定是相等的 |
| D.两个物体间的引力总是大小相等,方向相反的,是一对平衡力 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| A.月球比“天宫一号”速度大 | B.月球比“天宫一号”周期长 |
| C.月球比“天宫一号”角速度大 | D.月球比“天宫一号”加速度大 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
A.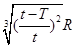 | B. | C. | D. |
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
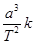 ,
, 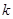 是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量
是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量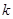 的表达式。已知引力常量为G,太阳的质量为M太。
的表达式。已知引力常量为G,太阳的质量为M太。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com