
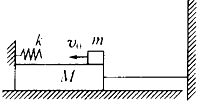
 ��ͼ��ʾ������ΪM�ij����龲ֹ�ڹ⻬ˮƽ���ϣ����̶�һ����ϵ��k�㹻���ˮƽ���ʵ��ɣ��Ҳ���һ�����쳤��ϸ������������ֱǽ�ϣ�ϸ�����ܳ��ܵ��������ΪT��ʹһ����Ϊm�����ٶ�Ϊv0��С��飬�ڻ�������Ħ��������������ѹ�����ɣ������ɵ������ܵı���ʽEp=
��ͼ��ʾ������ΪM�ij����龲ֹ�ڹ⻬ˮƽ���ϣ����̶�һ����ϵ��k�㹻���ˮƽ���ʵ��ɣ��Ҳ���һ�����쳤��ϸ������������ֱǽ�ϣ�ϸ�����ܳ��ܵ��������ΪT��ʹһ����Ϊm�����ٶ�Ϊv0��С��飬�ڻ�������Ħ��������������ѹ�����ɣ������ɵ������ܵı���ʽEp=| 1 |
| 2 |
| T | ||
|
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| x | 2 0 |
| T | ||
|
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| x | 2 0 |
|
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| kx |
| M |
| 1 |
| M |
|
| 1 |
| 2 |
| 1 |
| 2 |
| V | 2 1 |
| T | ||
|
| T | ||
|
| T | ||
|
| 1 |
| M |
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ������ΪM��б�������ˮƽ���ϣ�����������Ϊm��С��飬���Ӵ������Ħ��������һ�ν�ˮƽ��F1����M�ϣ��ڶ��ν�F2����m�ϣ����ζ�Ҫ��m��M��������Ի�������F1��F2�ı�Ϊ��������
��ͼ��ʾ������ΪM��б�������ˮƽ���ϣ�����������Ϊm��С��飬���Ӵ������Ħ��������һ�ν�ˮƽ��F1����M�ϣ��ڶ��ν�F2����m�ϣ����ζ�Ҫ��m��M��������Ի�������F1��F2�ı�Ϊ���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ������Ϊm��С��ˮƽ���Ϊ2mʱ���ٶȵĴ�СΪ4m/s��������ֱ���£�������˶��п��������Ĵ�С����������0.1��������������Ĺ����в���ʧ��е�ܣ���
��ͼ��ʾ������Ϊm��С��ˮƽ���Ϊ2mʱ���ٶȵĴ�СΪ4m/s��������ֱ���£�������˶��п��������Ĵ�С����������0.1��������������Ĺ����в���ʧ��е�ܣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ������Ϊm��С��A���ɾ�ֹ��ʼ�������䣬���ٶȴ�СΪ
��ͼ��ʾ������Ϊm��С��A���ɾ�ֹ��ʼ�������䣬���ٶȴ�СΪ| g |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ������ΪM����ͨ�������ֽ�����Ϊm�������Լ��ٶ�a���ᣬ�����������̣��˱��־�ֹ����������ֱ����н�Ϊ�ȣ���
��ͼ��ʾ������ΪM����ͨ�������ֽ�����Ϊm�������Լ��ٶ�a���ᣬ�����������̣��˱��־�ֹ����������ֱ����н�Ϊ�ȣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
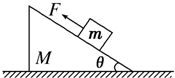 ��ͼ��ʾ������ΪM��Ш����龲ֹ��ˮƽ�����ϣ���б������Ϊ�ȣ�б������һ����Ϊm��С��飬С�����б��֮�����Ħ�����ú���F��б����������ʹ֮�����ϻ�����С����˶��Ĺ����У�Ш�����ʼ�ձ��־�ֹ��������
��ͼ��ʾ������ΪM��Ш����龲ֹ��ˮƽ�����ϣ���б������Ϊ�ȣ�б������һ����Ϊm��С��飬С�����б��֮�����Ħ�����ú���F��б����������ʹ֮�����ϻ�����С����˶��Ĺ����У�Ш�����ʼ�ձ��־�ֹ��������| A�������Ш������֧����Ϊ��M+m��g | B�������Ш������Ħ����Ϊ�� | C��Ш������С���Ħ��������Ϊ�� | D��С���һ���ܵ��ĸ������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com