
| A. | 1:2 | B. | 2:1 | C. | 3:2 | D. | 4:1 |
分析 在忽略自转的情况下,万有引力等于物体所受的重力,所以根据重力之比,可以求出中心天体的半径之比.
解答 解:在忽略地球自转的情况下,万有引力等于物体的重力${G}_{地}^{\;}=G\frac{{M}_{地}^{\;}m}{{R}_{地}^{2}}$①
在行星表面有${G}_{行}^{\;}=G\frac{{M}_{行}^{\;}m}{{R}_{行}^{2}}$②
联立①②得$\frac{{G}_{地}^{\;}}{{G}_{行}^{\;}}=\frac{{M}_{地}^{\;}}{{M}_{行}^{\;}}\frac{{R}_{行}^{2}}{{R}_{地}^{2}}$
代入数据得:$\frac{{R}_{行}^{\;}}{{R}_{地}^{\;}}=2$,故B正确,ACD错误;
故选:B
点评 忽略自转的情况下万有引力等于物体所受的重力,这是经常用的方法要注意掌握.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
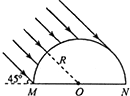 将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
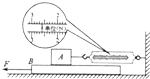 某学习小组测量动摩擦因数,将长木板B置于水平面上,物块A置于B板上,一轻弹簧秤右端固定,左端挂钩与A相连,弹簧秤水平,已知物块A的质量为0.8kg,当地重力加速度g=9.8m/s2.用水平力F向左拉木板B,使其向左运动,弹簧秤的放大情况如图所示,其读数为2.60N,A、B间的动摩擦因数μ=0.332(保留三位有效数字),木板B运动过程中,不需要(填“需要”或“不需要”)匀速直线运动.
某学习小组测量动摩擦因数,将长木板B置于水平面上,物块A置于B板上,一轻弹簧秤右端固定,左端挂钩与A相连,弹簧秤水平,已知物块A的质量为0.8kg,当地重力加速度g=9.8m/s2.用水平力F向左拉木板B,使其向左运动,弹簧秤的放大情况如图所示,其读数为2.60N,A、B间的动摩擦因数μ=0.332(保留三位有效数字),木板B运动过程中,不需要(填“需要”或“不需要”)匀速直线运动.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B. | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C. | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D. | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
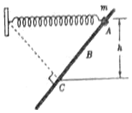 如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 上滑经过B的速度大于下滑经过B的速度 | |
| C. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| D. | 在A处,弹簧的弹性势能为mgh-$\frac{1}{4}$mv2 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
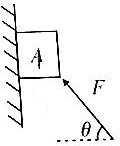 如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )| A. | 物体A受到4个力作用 | B. | mg=Fcosθ | ||
| C. | 物体A对墙的压力为Fcosθ | D. | 撤去F后,物体A做自由落体运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com