一炮艇总质量为M，以速度匀速行驶，从船上以相对海岸的水平速度沿前进方向射出一质量为m的炮弹，发射炮弹后艇的速度为，若不计水的阻力，则下列各关系式中正确的是         。（填选项前的编号）

①      　　　　   ②

③            ④

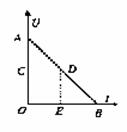
如图所示，为测电源电动势和内电阻时，依据测量数据做出的路端电压与电流强度的关系图线，由图DC平行于横坐标轴，DE平行于纵坐标轴，由图可知（   ）

A．比值表示外电路电阻    

B．比值表示电源内电阻

C．比值表示电源电动势   

D．矩形OCDE的面积表示电源的输出功率

关于平抛运动，下列说法正确的是（      ）

A．平抛运动是匀变速运动

B．平抛运动是变加速运动

C．任意两段时间内加速度相同

D．任意两段相等时间内速度变化相同

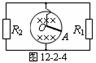如图12-2-4所示，在磁感强度为B的匀强磁场中有一半径为L的金属圆环．已知构成圆环的电线电阻为4r₀，以O为轴可以在圆环上滑动的金属棒OA电阻为r₀，电阻R₁=R₂=4r₀．当OA棒以角速度匀速转动时，电阻R₁的电功率最小值为P₀为多大？（其它电阻不计）

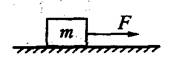如图所示，在水平地面上静置一质量为m=2.0kg的物块，现对物块施加一水平向右的拉力，物块开始向右做匀加速直线运动；过一段时间后，保持拉力的方向不变，大小变为，物块开始做匀减速直线运动．若加速与减速运动的时间和位移的大小均相等，则物块与地面间的动摩擦因数为      。g=10m/s²

一辆质量为4t的汽车，发动机的额定功率为80KW，所受阻力为车重的0.1倍。如果汽车从静止开始在平直公路上做匀加速运动，当功率达到额定功率后，又以额定功率运动了一段距离，汽车达到最大速度，在整个过程中，汽车运动了125m。试求在整个过程中，汽车发动机的牵引力做了多少功？（取g=10m/s²）

关于运动的合成与分解，以下说法正确的是（      ）

A．由两个分运动求合运动，合运动是唯一确定的

B．由合运动分解为两个分运动，可以有不同的分解方法

C．物体做曲线运动时，才能将这个运动分解为两个分运动

D．任何形式的运动，都可以用几个分运动代替

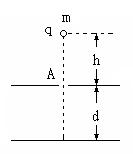
如图所示，平行板电容器两板间距离为d，所带电量为Q，且上极板带正电。一质量为m，带电量为q的小球，在离平行板电容器上极板小孔A的正上方h处自由释放，到达下极板时小球的速度恰好为零（小球不与下极板接触）。已知重力加速度为g。

（1）试分析小球所带电荷的性质，并简要说明小球的运动过程。

（2）小球开始下落到速度减为零的过程中所用的时间和最大速度分别为多少？

（3）电容器的电容为多少？

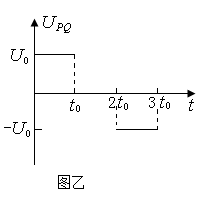
如图甲所示，建立Oxy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，第一四象限有磁场，方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0~3t时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）。

已知t=0时刻进入两板间的带电粒子恰好在t₀时，刻经极板边缘射入磁场。上述m、q、l、l₀、B为已知量。（不考虑粒子间相互影响及返回板间的情况）

（1）求电压U的大小。

（2）求时进入两板间的带电粒子在磁场中做圆周运动的半径。

（3）何时把两板间的带电粒子在磁场中的运动时间最短？求此最短时间。

“神舟”六号飞船完成了预定空间科学和技术试验任务后，返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回。在离地l0km的高度返回舱打开阻力降落伞减速下降，返回舱在这一过程中所受空气阻力与速度的平方成正比，比例系数（空气阻力系数）为k。已知返回舱的总质量M =3000kg，所受空气浮力恒定不变，且认为竖直降落。从某时刻起开始计时，返回舱的运动v — t图象如图中的AD曲线所示，图中AB是曲线在A点的切线，切线交于横轴于B点的坐标为（ 10，0 ），CD是AD的渐近线，亦是平行于横轴的直线，交纵轴于C点，C点的坐标为（ 0，6 ）。请解决下列问题：（取g=10 m/ s²）

   （1）在初始时刻v₀ = 160m/s时，它的加速度多大?

   （2）推证空气阻力系数k的表达式并算出其数值；

   （3）返回舱在距地高度h = 10m时, 飞船底部的4个反推力小火箭点火工作, 使其速度由6m/s迅速减至1m/s后落在地面上。 若忽略燃料质量的减少对返回舱总质量的影响, 并忽略此阶段速度变化而引起空气阻力的变化, 试估算每支小火箭的平均推力（计算结果取两位有效数字）。