
1.设集合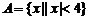 ,
, ,则集合{
,则集合{ 且
且 }=
。
}=
。
2.下列说法中:(1)若 ,则
,则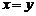 ;(2)等比数列是递增数列的一个必要条件是公比大于1;
;(2)等比数列是递增数列的一个必要条件是公比大于1;
(3) 的否定是;(4)若
的否定是;(4)若 ,则
,则 或
或 。其中不正确的有 。
。其中不正确的有 。
3.设集合 ,
, ,且
,且 ,则实数
,则实数 的取值范围是 。
的取值范围是 。
4.已知二次函数 满足
满足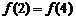 ,则
,则 = 。
= 。
5.计算: = 。
= 。
6.已知函数 的值域是[-1,4 ],则
的值域是[-1,4 ],则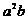 的值是
。
的值是
。
7.若函数 ,
, 的图象关于直线
的图象关于直线 对称,则
对称,则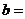 。
。
8.函数 的图象与
的图象与 的图象关于直线y=x对称,那么
的图象关于直线y=x对称,那么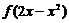 的单调减区
的单调减区
间是 。
9.函数 的反函数
的反函数 的图象的对称中心是(-1,3),则实数a=
。
的图象的对称中心是(-1,3),则实数a=
。
10. 是R上的减函数,且
是R上的减函数,且 的图象经过点A(0,1)和B(3,-1),则不等式
的图象经过点A(0,1)和B(3,-1),则不等式
 的解集为
。
的解集为
。
11.已知函数 ,若
,若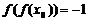 ,则
,则 的取值范围是
.
的取值范围是
.
12.已知函数 如果
如果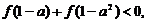 则
则 的取值范围是____。
的取值范围是____。
13.关于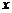 的方程
的方程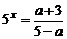 有负根,则a的取值范围是
。
有负根,则a的取值范围是
。
14.已知函数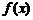 满足:对任意实数
满足:对任意实数 ,当
,当 时,有
时,有 ,且
,且
 写出满足上述条件的一个函数:
。
写出满足上述条件的一个函数:
。
15.定义在区间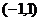 内的函数
内的函数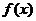 满足
满足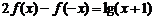 ,则
,则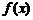 =
。
=
。
16.已知函数 ,
,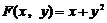 ,则
,则 等于
。
等于
。
17.对任意 ,函数
,函数 的值恒大于零,那么
的值恒大于零,那么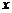 的取值范围是 。
的取值范围是 。
18.若函数 ,其中
,其中 表示
表示 两者中的较小者,则
两者中的较小者,则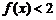 的解为 。
的解为 。
19.已知函数f (x)=log2(x+1),若-1<a<b<c,且abc≠0,则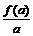 、
、 、
、 的大小关系是 。
的大小关系是 。
20.若方程 有解,则实数
有解,则实数 的取值范围是 .
的取值范围是 .
21.等差数列 前n项之和为
前n项之和为 ,若
,若 ,则
,则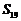 的值为
。
的值为
。
22.已知数列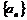 中,
中, ,那么
,那么 的值为 。
的值为 。
23.已知等差数列 前n项的和
前n项的和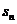 ,若
,若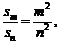 则
则 的值是
。
的值是
。
24.已知一个等差数列前五项的和是120,后五项的和是180,又各项之和是360,则此数列共有 项。
25.设等比数列 中,每项均是正数,且
中,每项均是正数,且 ,则
,则

。
26.一个项数为偶数的等比数列,首项是1,且所有奇数项之和是85,所有偶数项之和是170,则此数列共有 项。
27.设 ,利用课本中推导等差数列前n项和的公式的方法,可求得:
,利用课本中推导等差数列前n项和的公式的方法,可求得:
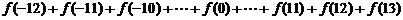 的值为
的值为
28.已知数列 的通项
的通项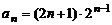 ,前n项和为
,前n项和为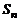 ,则
,则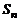 =
。
=
。
29.数列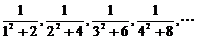 前n项的和等于
。
前n项的和等于
。
30.数列 中,
中, ,则其通项公式为
,则其通项公式为 。
。
高考数学基础训练题(2)
31.函数 的图象按向量
的图象按向量 平移后,所得函数的解析式是
平移后,所得函数的解析式是 ,则
,则 =
=
(只需写出满足条件的一个向量)
32.函数 的图象相邻的两条对称轴间的距离是
。
的图象相邻的两条对称轴间的距离是
。
33.函数 的单调增区间是
。
的单调增区间是
。
34.已知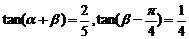 ,则
,则 。
。
35. =_______________。
=_______________。
36.函数 的最大值是
。
的最大值是
。
37.已知 则
则 。
。
38.已知 则
则 __ __。
__ __。
39.如果 ,那么函数
,那么函数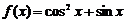 的最小值是
。
的最小值是
。
40.函数 的最大值为
。
的最大值为
。
41.已知 ,则
,则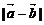 =
。
=
。
42.若非零向量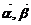 满足
满足 ,则
,则 与
与 所成角的大小为 。
所成角的大小为 。
43.与向量 平行的单位向量是_____________。
平行的单位向量是_____________。
44.在直角坐标平面上,向量 ,向量
,向量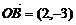 ,两向量在直线
,两向量在直线 上的正射影长度相等,则直线
上的正射影长度相等,则直线 的斜率为
的斜率为
45.设平面向量 =(-2,1),
=(-2,1),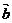 =(1,
=(1, ),若
),若 与
与 的夹角为钝角,则
的夹角为钝角,则 的取值范围是
。
的取值范围是
。
46.已知向量 ,则向量
,则向量 的夹角范围是
的夹角范围是
。
47.将函数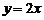 的图象按向量
的图象按向量  平移后得到
平移后得到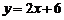 的图象,给出以下四个命题:
的图象,给出以下四个命题:
① 的坐标可以是
的坐标可以是 ; ②
; ② 的坐标可以是
的坐标可以是 和
和 ;
;
③ 的坐标可以是
的坐标可以是 ; ④
; ④ 的坐标可以有无数种情况。
的坐标可以有无数种情况。
上述说法正确的是 。
48.某人在静水中游泳的速度为4千米/时,水的流向是由西向东,水流速度为2 千米/时,则此人必须朝与水流方向成__*___度角时,才能沿正北方向前进 。
千米/时,则此人必须朝与水流方向成__*___度角时,才能沿正北方向前进 。
49.在△ABC中,BC=1,∠B= ,当△ABC的面积为
,当△ABC的面积为 时,
时, 。
。
50.若△ABC三边长AB=5,BC=7,AC=8,则 等于
。
等于
。
51.函数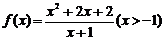 的图象的最低点的坐标是 。
的图象的最低点的坐标是 。
52.已知正实数 满足
满足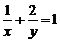 ,则
,则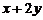 的最小值为_________________。
的最小值为_________________。
53.设实数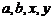 满足
满足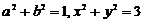 , 则
, 则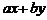 的取值范围为____________。
的取值范围为____________。
54.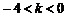 是函数
是函数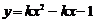 恒为负值的___________条件。
恒为负值的___________条件。
55.不等式 的解集是
。
的解集是
。
56. 若不等式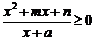 的解集为
的解集为 ,则
,则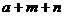 =
=
57.关于 的不等式
的不等式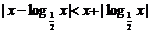 的解集为
。
的解集为
。
58.若 ,
, ,且
,且 ,则实数
,则实数 的范围是 .
的范围是 .
59.若不等式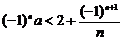 对于任意正整数
对于任意正整数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
60.实系数一元二次方程 的两根分别在区间
的两根分别在区间 和
和 上,则
上,则 的取值范围是
的取值范围是
 高考数学基础训练题(3)
高考数学基础训练题(3)
61.从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有 个。(用数字作答)
62.某小组有4个男同学和3个女同学,从这小组中选取4人去完成三项不同的工作,其中女同
学至少二人,每项工作至少一人,则不同选派方法的种数为 。
63.现有8名青年,其中有5名青年能胜任英语翻译工作,4名青年能胜任电脑软件设计工作,(其中有一人两项工作都能胜任),现要从中选派5名青年承担一项任务,其中3人从事英语翻译工作,2人从事软件设计工作,则不同的选法种数为 。
64.6人站成一排照相,其中甲,乙,丙三人要站在一起,并且乙,丙要站在甲的两边,则不同的排法种数共有 种。
65. 现有6个参加兴趣小组的名额,分给4个班级,每班至少一个,则不同的分配方案共有_____种。
66.把6本书平均分给甲、乙、丙3个人,每人2本,有 种分法,若平均分成3份,每份2本,有 种分法。
67.从集合 中选3个不同的数,使这3个数成递增的等差数列,则这样的数列共有_______组。
中选3个不同的数,使这3个数成递增的等差数列,则这样的数列共有_______组。
68.从6双不同的手套中任取4只,其中恰有一双配对的取法有_______种。
69.从6个正方形拼成的右图的12个顶点中任取3个顶点作为一组,
其中可以构成三角形的组数为 。
70、某幢楼从二楼到三楼的楼梯共10级,上楼可以一步上一级,也可以一步上两级,若规定从二楼到三楼用8步走完,则上楼梯的方法有 。
71.
 展开式中,
展开式中, 的系数是
。
的系数是
。
72.设函数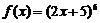 ,则导函数
,则导函数
 中的
中的 的系数是
的系数是
73.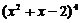 展开式中
展开式中 项的系数是
。
项的系数是
。
74. ,则
,则 =
。
=
。
75.若 ,则
,则 =
。
=
。
76.坛中有红球6个,白球4个,今从中任取3个,至少取到一个白球的概率为______.
77.从1,2,…..,9这九个数中,随机取2个不同的数,则这两个数的和为偶数的概率是 。
78.制造一个零件,甲机床的废品率是0.04,乙机床的废品率是0.05,从它们制造的产品中各任取一件,其中恰有一件废品的概率是 。
79.有一数学问题,在半小时内,甲能解决它的概率为 ,乙能解决它的概率为
,乙能解决它的概率为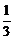 ,如果两人都试图独立地在半小时内解决它,则两人都未解决的概率是 ,问题得到解决的概率是 。
,如果两人都试图独立地在半小时内解决它,则两人都未解决的概率是 ,问题得到解决的概率是 。
80.一台X型号自动机床在一小时内不需要工人照看的概率为0.8,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 。
81.设两个独立事件A和B都不发生的概率为 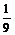 ,A发生B不发生的概率和B发生A不发生的概率相同,则事件A发生的概率为
。
,A发生B不发生的概率和B发生A不发生的概率相同,则事件A发生的概率为
。
82.已知一个样本方差为 ,则这个样本的容量是________,平均数是____________.
,则这个样本的容量是________,平均数是____________.
83.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4 ,9.9 ,9.6 ,9.4 ,
9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 、 。
84.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验. 利用随机数表抽取样本时,先将800袋牛奶按000, 000,…, 799进行编号,如果从随机数表第8行第7列的数开始向右读,请你依次写出最先检测的5袋牛奶的编号 .
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
85.函数 的递增区间为________________
的递增区间为________________
86.设点 是曲线
是曲线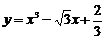 上的任意一点,
上的任意一点, 点处切线倾斜角为
点处切线倾斜角为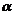 ,则角
,则角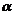 的取值范围
的取值范围
是 。
87.垂直于直线 且与曲线
且与曲线 相切的直线方程的一般式__________.
相切的直线方程的一般式__________.
88.函数 在点x=1处有极小值-1,则
在点x=1处有极小值-1,则 =
,
=
,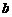 =
。
=
。
89.已知函数 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数 的取值范围是
的取值范围是
。
90.已知: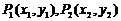 都在曲线
都在曲线 上,且过P2点的曲线的切线经过P1点,若
上,且过P2点的曲线的切线经过P1点,若
 ,则
,则 ___________。
___________。
 高考数学基础训练题(4)
高考数学基础训练题(4)
91.已知直线 ,
, 过点
过点 ,并且它们的方向向量
,并且它们的方向向量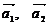 满足
满足 ,那么
,那么 的方程是
。
的方程是
。
92.若平面上两点A(-4,1),B(3,-1),直线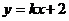 与线段AB恒有公共点,则k的取值范围是
。
与线段AB恒有公共点,则k的取值范围是
。
93.已知△ABC的顶点A(1,4),若点B在y轴上,点C在直线y=x上,则△ABC的周长的最小值是 。
94.设过点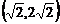 的直线l的斜率为k,若圆
的直线l的斜率为k,若圆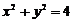 上恰有三点到直线l的距离等于1,则k的值是
。
上恰有三点到直线l的距离等于1,则k的值是
。
95.直线 与
与 是圆的两条切线,则该圆的面积是
是圆的两条切线,则该圆的面积是
96.过定点(1,2)总可作两直线与圆 相切,则k的取值范围是 。
相切,则k的取值范围是 。
97.椭圆 上的一点P到它的右准线的距离是10,那么P到它的左焦点的距离是
上的一点P到它的右准线的距离是10,那么P到它的左焦点的距离是
98.已知定点 ,F是椭圆
,F是椭圆 的左焦点,点M在椭圆上,若使
的左焦点,点M在椭圆上,若使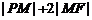 最小,则点M的坐标为 。
最小,则点M的坐标为 。
99.若椭圆 的左、右焦点分别为
的左、右焦点分别为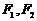 ,抛物线
,抛物线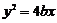 的焦点为
的焦点为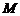 ,若
,若 ,则此椭圆的离心率为
,则此椭圆的离心率为
100.当m满足
时,曲线 与曲线
与曲线 的焦距相等.
的焦距相等.
101.已知双曲线 的右顶点为A,而B、C是双曲线右支上两点,若三角形ABC
的右顶点为A,而B、C是双曲线右支上两点,若三角形ABC
为等边三角形,则m的取值范围是 。
102.经过双曲线 上任一点
上任一点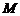 ,作平行于实轴的直线,与渐近线交于
,作平行于实轴的直线,与渐近线交于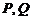 两点,则
两点,则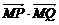 =
=
103.一个动圆的圆心在抛物线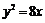 上,且动圆恒与直线
上,且动圆恒与直线 相切,则此动圆必经过点 。
相切,则此动圆必经过点 。
104.过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在抛物线准线上的射影分别为
A1、B1,则∠A1FB1= 。
105.长度为 的线段AB的两个端点A、B都在抛物线
的线段AB的两个端点A、B都在抛物线 上滑动,则线段
上滑动,则线段
AB的中点M到y轴的最短距离为 。
106.在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的大小等于 。(结果用反三角函数值表示)
107.点A、B到平面 距离分别为12,20,若斜线AB与
距离分别为12,20,若斜线AB与 成
成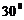 的角,则AB的长等于_____。
的角,则AB的长等于_____。
108.已知PA、PB、PC是从P点出发的三条射线,每两条射线的夹角均为600,则直线PC与平
面PAB所成角的余弦值是 。
109.从空间一个点P引四条射线PA、PB、PC、PD,它们两两之间的夹角相等,则该角的余弦
值为 。
110.已知△ABC中,AB=9,AC=15,∠BAC=1200,这三角形所在平面α外的一点P与三个顶
点的距离都是14,那么P到平面α的距离是 。
111.在平面角为600的二面角 内有一点P,P到α、β的距离分别为PC=2cm,
内有一点P,P到α、β的距离分别为PC=2cm,
PD=3cm,则P到棱l的距离为____________。
112.
在平面α内有一个正△ABC,以BC边为轴把△ABC旋转θ角,θ∈(0, ),得到△A'BC,当cosθ=
),得到△A'BC,当cosθ=
时,△A'BC在平面α内的射影是直角三角形。
113.三棱柱的一个侧面面积为S,此侧面所对的棱与此面的距离为h,则此棱柱的体积为 。
114.已知空间三个平面 两两垂直,直线
两两垂直,直线 与平面
与平面 所成的角都是
所成的角都是 ,则直线
,则直线 与平面
与平面 所成角的是 .
所成角的是 .
115.在正三棱锥S-ABC中,侧棱SC⊥侧面SAB,侧棱SC= ,则此正三棱锥的外接球的表面积为
。
,则此正三棱锥的外接球的表面积为
。
116.给定一个正方体与三个球,其中一个球与该正方体的各面都相切,第二个球与正方体的各棱都相切,第三个球过正方体的各个顶点,则此三球的半径之比是 。
117.某地球仪上北纬 ,纬线的长度为
,纬线的长度为 ,该地球仪的半径是____cm,表面积是
cm2。
,该地球仪的半径是____cm,表面积是
cm2。
118.在北纬450圈上有M、N两点,点M在东经200,N在西经700,若地球半径是R,则M、N两点的球面距离是
119. 自半径为R的球面上一点P引球的两两垂直的弦PA、PB、PC,则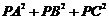 =_____。
=_____。
120.球面上有三个点A、B、C组成球的一个内接三角形,若AB=18,BC=24,AC=30,且球
心到△ABC所在平面的距离等于球半径的 ,那么这个球的表面积是
。
,那么这个球的表面积是
。
高考数学基础训练题(1)参考答案
高考数学基础训练题参考答案
基础训练题(1)
1、[1,3] ;2、(1)(2)(3);3、[0,1];4、-3;5、0;6、48;7、6;8、(0,1];9、2;10、(-1,2);
11、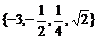 ;12、
;12、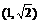 ;13、(-3,1);14、
;13、(-3,1);14、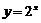 ;15、
;15、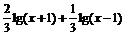 ;16、
;16、 ;
;
17、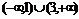 ;18、
;18、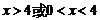 ;19、
;19、 ;20、
;20、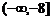 ;21、95;22、765;
;21、95;22、765;
23、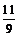 ;24、12;25、20; 26、8;27、
;24、12;25、20; 26、8;27、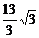 ;28、
;28、 ;29、
;29、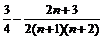 ;
;
30、 ;
;
基础训练题(2)
31、 ;32、
;32、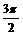 ; 33、
; 33、 ; 34、
; 34、 ; 35、
; 35、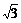 ;36、7;37、
;36、7;37、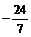 ;
;
38、 ;39、
;39、 ;40、
;40、 ;41、
;41、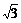 ;42、900;43、
;42、900;43、 ,
,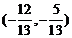 ; 44、
; 44、 ;
;
45、 ;46、
;46、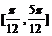 ; 47、①②③④ ;48、135;49、
; 47、①②③④ ;48、135;49、 ;50、
;50、 ;
;
51、(0,2);52、9; 53、 ;
54、充分非必要;55、
;
54、充分非必要;55、 ;
56、-4; 57、(0,1);
;
56、-4; 57、(0,1);
58、 ;59、
;59、 ; 60、
; 60、 ;
;
基础训练题(3)
61、300;62、792;63、42;64、48;65、10;66、90,15;67、90;68、240;69、200;70、28;
71、 ;72、24000;73、-8;74、242;75、
;72、24000;73、-8;74、242;75、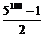 ;76、
;76、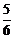 ;77、
;77、 ;78、0.086;
;78、0.086;
79、 ;80、0.9728;81、
;80、0.9728;81、 ;82、10,4;83、
;82、10,4;83、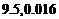 ;84、
;84、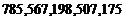 ;
;
85、 ;86、
;86、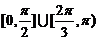 ;87、
;87、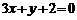 ;88、
;88、 ;89、
;89、 ;90、
;90、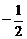 ;
;
基础训练题(4)
91、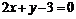 ; 92、
; 92、 ; 93、
; 93、 ; 94、1或7;95、
; 94、1或7;95、 ;96、
;96、 ;
;
97、12;98、 ;99、
;99、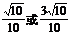 ;100、m<9且m≠6且m≠5 ;101、
;100、m<9且m≠6且m≠5 ;101、 ;102、
;102、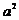 ;103、
;103、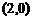 ;104、
;104、 ;105、
;105、 ;106、
;106、 ;107、16或64;108、
;107、16或64;108、 ;109、
;109、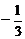 ;
;
110、7;111、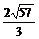 ;112、
;112、 ;113、
;113、 ;114、
;114、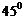 ;115、
;115、 ;116、
;116、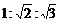 ;117、
;117、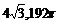 ;
;
118、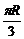 ;119、
;119、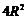 ;120、1200π;
;120、1200π;