
1. 在R上定义运算 若不等式
若不等式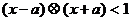 对任意实数
对任意实数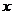 成立,则
成立,则
A.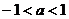 B.
B. C.
C. D.
D.
2.  如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是

3. 在平面直角坐标系中,x轴正半轴上有5个点, y轴正半轴有3个点,将x轴上这5个点和y轴上这3个点连成15条线段,这15条线段在第一象限内的交点最多有
A.30个 B.35个 C.20个 D.15个
4. 定义集合A*B={x|x A,且x
A,且x B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为
B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为
A.1 B.2 C.3 D.4
5. 已知a,b,c,d均为实数,有下列命题:

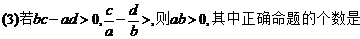
A. 0 B. 1 C.2 D. 3
6. 已知集合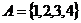 ,集合
,集合 ,设映射
,设映射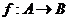 ,如果集合B中的元素都是A中元素的f下的象,那么这样的映射f有
,如果集合B中的元素都是A中元素的f下的象,那么这样的映射f有
A.16个 B.14个 C.12个 D.8个
7. 已知函数f(x)满足:f(p+q)= f(p)f(q),f(1)= 3,则 +
+ +
+
+ +
+ 的值为
的值为
A.15 B.30 C.75 D.60
8. 若A.、B均是非空集合,则A∩B≠φ是A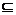 B的
B的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.即不充分也不必要条件
9. 在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为
A.0.5 B.1 C.2 D. 4
10. ab>ac是b>c的
A.充分不必要条件 B. 必要不充分条件 C.充要条件 D.即不充分也不必要条件
第Ⅱ卷(非选择题 共5道填空题6道解答题)
请将你认为正确的答案代号填在下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| | | | | | | | | | |
11. 已知抛物线y2=a(x+1)的准线方程是x= -3,那么抛物线的焦点坐标是______.
12. 给出下列图象


其中可能为函数f(x)=x4+ax3+bx2+cx+d(a,b,c,d∈R)的图象的是_____.
13. 已知f(x)=ax(a>1),g(x)=bx(b>1),当f(x1)=g(x2)=2时,
有x1>x2,则a,b的大小关系是 .
14. 正三棱锥P-ABC的四个顶点同在一个半径为2的球面上,若正三棱锥的侧棱长为2,则正三棱锥的底面边长是____________.
15. 设正数数列{an}的前n项和为Sn,且存在正数t,使得对于所有自然数n,有
16. 已知a=(cos ,sin
,sin ),b=(cos
),b=(cos ,sin
,sin ),其中0<
),其中0< <
< <
< .(1)求证:a+b 与a-b互相垂直; (2)若ka+b与a-kb的长度相等,求
.(1)求证:a+b 与a-b互相垂直; (2)若ka+b与a-kb的长度相等,求 -
- 的值(k为非零的常数).
的值(k为非零的常数).
17. 一个医生已知某种病患者的痊愈率为25%,为试验一种新药的效果,把它给10个
病人服用,且规定若10个病人中至少有4个被治好,则认为这种试验有效;反之,
则认为试验无效。若服用新药后,病患者的痊愈率提高,则认为新药有效;反之,
则认为新药无效.试求:
(I)虽新药有效,且把痊愈率提高到35%,但通过试验被否定的概率.
(II)新药完全无效,但通过试验被认为有效的概率.(精确到0.001)
18. 在Rt△ABC中,∠ACB=30°,∠B=90°,D为AC中点,E为BD的中点,AE的延长线交
BC于F,将△ABD沿BD折起,二面角A-BD-C大小记为θ.
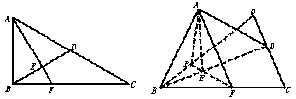 (Ⅰ)求证:面AEF⊥面BCD;
(Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD.
19. 
20. 已知动圆过定点P(1,0),且与定直线L:x=-1相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;

(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
21. 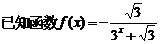
(1)求证:函数y=f(x)的图象关于点(0.5,-0.5)对称;
(2)求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值;
高三综合测试(二)参考答案

参考答案
一.选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | B | A | D | D | B | B | B | C | D |
3. 交点的个数个数等于在x、y各取两点构成的四边形的个数
二.填空题
11. (1,0)
12. ①③
13. a<b
14. 3
15. 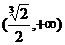
三.解答题
16. (1)由题意得:a+b=(cos α+cos β,sin α+sin β)a-b=(cos α-cos β, sin α-sin β) 3分∴(a+b).(a-b)=(cos α+cos β)(cos α-cos β)+(sin α+sin β)(sin α-sin β)=cos2α-cos2β+sin2α-sin2β=1-1=0∴a+b 与a-b互相垂直. 6分
(2) 方法一:ka+b=(kcos α+cos β,ksin α+sin β),a-kb=(cos α-kcos β, sin α-ksin β) 8分| ka+b |=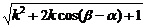 ,| a-kb |=
,| a-kb |= 9分由题意,得4cos (β-α)=0,因为0<α<β<π ,所以β-α=
9分由题意,得4cos (β-α)=0,因为0<α<β<π ,所以β-α= . 12分
. 12分
方法二:由| ka+b |=| a-kb |得:| ka+b |2=| a-kb |2即(ka+b )2=( a-kb )2,k2| a |2+2ka×b+| b |2=| a |2-2ka×b+k2| b |2 8分由于| a|=1,| b |=1∴k2+2ka×b+1=1-2ka×b+k2,故a×b=0,即(cos ,sin
,sin )× (cos
)× (cos ,sin
,sin )=0 10分Þ
)=0 10分Þ  因为0<α<β<π ,所以β-α=
因为0<α<β<π ,所以β-α= . 12分
. 12分
17. (I)0.514 (II)0.224
18. (Ⅰ)证明:在Rt△ABC中,∠C=30°,D为AC的中点,则△ABD是等边三角形
又E是BD的中点,∵BD⊥AE,BD⊥EF,折起后,AE∩EF=E,∴BD⊥面AEF
∵BD 面BCD,∴面AEF⊥面BCD
面BCD,∴面AEF⊥面BCD
(Ⅱ)解:过A作AP⊥面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,
令AB=1,则△ABD是边长为1的等边三角形,若AB⊥CD,则BQ⊥CD

由于∠AEF=θ就是二面角A-BD-C的平面角,

19. 设 ,则
,则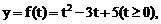 f(t)的顶点横坐标为
f(t)的顶点横坐标为 ,属于
,属于 ,故f(t)在
,故f(t)在 上是减函数,在
上是减函数,在 为增函数,所以最小值在
为增函数,所以最小值在 达到,为
达到,为 ,当
,当 时达到最小值
时达到最小值 ,该函数没有最大值
,该函数没有最大值
20. (1)依题意,曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为y2=4x.

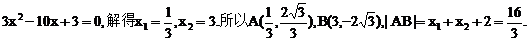
假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,即

因此,直线l上不存在点C,使得△ABC是正三角形.
(ii)解法一:设C(-1,y)使△ABC成钝角三角形,
 ,
,
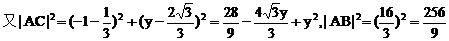 ,
,

∠CAB为钝角.



 .
.
该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是:
 .
.
解法二:以AB为直径的圆的方程为:
 .
.

当直线l上的C点与G重合时,∠ACB为直角,当C与G 点不重合,且A,
B,C三点不共线时, ∠ACB为锐角,即△ABC中∠ACB不可能是钝角.
因此,要使△ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.
 .
.
 .
.

A,B,C三点共 线,不构成三角形.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是:

21. (1)设P(x,y)是y=f(x)的图象上任意一点,
关于(0.5,-0.5)对称点的坐标为:(1-x,-1-y)
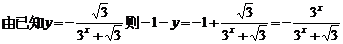

∴-1-y=f(1-x),即函数y=f(x)的图象关于点(0.5,-0.5)对称.
(2)由(Ⅰ)有f(1-x)=-1-f(x)即f(x)+f(1-x)= -1
∴f(-2)+f(3)=-1,f(-1)+f(2)=-1,f(0)+f(1)=-1
则f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)=-3
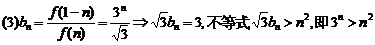
下面用数学归纳法证明
当n=1时,左=3,右=1,3>1不等式成立
当n=2时,左=9,右=4,9>4不等式成立
令n=k(k≥2)不等式成立即3k>k2
则n=k+1时,左=3k+1=3.3k>3.k2
右=(k+1)2=k2+2k+1
∵3k2-(k2+2k+1)=2k2-2k-1=2(k-0.5)2-1.5
当k≥2,k∈N时,上式恒为正值
则左>右,即3k+1>(k+1)2,所以对任何自然数n,总有3n>n2成立,即对任何自然数n,总有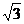 bn>n2成立
bn>n2成立