
网址:http://1010pic.com/paper/timu/5152304.html[举报]
5. 理解全称命题与特称命题的构成,能判断其真假;能写出含有一个全称量词与存在量词的的命题的否定。
II函数部分
[考纲要求]
(1)函数
① 了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.
② 在实际情境中,会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数.
③ 了解简单的分段函数,并能简单应用.
④ 理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解函数奇偶性的含义.
⑤ 会运用函数图像理解和研究函数的性质.
(2)指数函数
① 了解指数函数模型的实际背景.
② 理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
③ 理解指数函数的概念,理解指数函数的单调性,掌握指数函数图像通过的特殊点.
④ 知道指数函数是一类重要的函数模型.
(3)对数函数
① 理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
② 理解对数函数的概念;理解对数函数的单调性,掌握对数函数图像通过的特殊点.
③ 知道对数函数是一类重要的函数模型;
④ 了解指数函数 与对数函数
与对数函数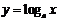 互为反函数(
互为反函数( ).
).
(4)幂函数
① 了解幂函数的概念.
② 结合函数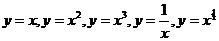 的图像,了解它们的变化情况.
的图像,了解它们的变化情况.
(5)函数与方程
① 结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.
② 根据具体函数的图像,能够用二分法求相应方程的近似解.
(6)函数模型及其应用
① 了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.
② 了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
[地位分析]函数是高中数学的重要内容,函数概念及其所反映的数学思想已经渗透到数学的各个领域:函数与代数式、函数与方程、函数与不等式、函数与数列、函数与圆锥曲线及函数与微积分都有密切的联系。因此函数的思想方法将贯穿高中数学课程的始终。
[课标与07年考纲比较]
|
《课程标准》 |
《考试大纲》 |
|
理解指数函数的特殊点. |
掌握指数函数图象通过的特殊点. |
|
了解对数函数的单调性与特殊点. |
理解对数函数的单调性,掌握对数函数图象通过的特殊点. |
[07年考纲与06年考纲的比较]
|
07考纲(新) |
06考纲(旧) |
|
了解构成函数的要素,会求一些简单函数的定义域和值域; |
理解函数的概念. |
|
了解简单的分段函数,并能简单应用. |
|
|
理解函数的单调性、最大值、最小值及其几何意义;结合具体函数,了解函数奇偶性的含义. |
掌握判断一些简单函数的单调性、奇偶性的方法. |
|
理解指数函数的概念,理解指数函数的单调性,掌握指数函数图像通过的特殊点. |
掌握指数函数的概念、图像和性质. |
|
知道用换底公式能将一般对数转化成自然对数或常用对数; |
|
|
理解对数函数的概念;理解对数函数的单调性,掌握对数函数图像通过的特殊点. |
掌握对数函数的概念、图像和性质. |
|
知道指数函数是一类重要的函数模型. 知道对数函数是一类重要的函数模型; |
能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题. |
了解指数函数 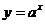 与对数函数 与对数函数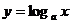 互为反函数( 互为反函数(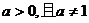 ) ) |
了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数. |
|
幂函数、函数与方程、函数模型及其应用 |
|
[新增内容]:函数的奇偶性、幂函数、函数的零点与方程的根、二分法求方程的近似根。
(1)函数的奇偶性由三角函数内容提升到函数部分,主要优化知识的系统性、完备性。
(2)幂函数要求层次较低,只要求能借助研究函数性质的思想方法,会探讨五个简单幂函数的性质。
(3)函数与方程是新课标新增内容课标要求的层次相对较低,但方程的根与函数的零点是“数形思想”的一个知识点,建议在这一部分适当推广到任意函数。结合图象补充一元二次不等式的解法,处理有关二次三项式大于零的恒成立问题。了解根的存在性定理,学会利用二分法求方程的近似根,体会算法思想。
[淡化内容]:映射(了解)、反函数(课本一带而过)。
[强化内容]:分段函数:课本用较大篇幅,借助大量例题分析如何建立分段函数模型,复习时应重视。
[课时建议]22课时.
[重点与难点]
参考答案
1.C 2. C 3.C
4.D 5.C 6.B 7.C
8.A 9. 6 10. 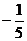
11. 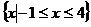 ;
;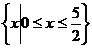 12. 4 13.
12. 4 13. 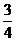 14. ①④⑤
14. ①④⑤
15. 解:由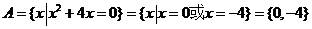 .
.
∵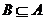 ,∴
,∴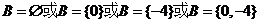 .
.
当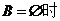 ,即
,即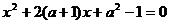 无实根,由
无实根,由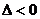 ,
,
即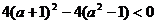 ,解得
,解得 ;
;
当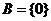 时,由根与系数的关系:
时,由根与系数的关系: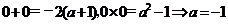 ;
;
当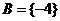 时,由根与系数的关系:
时,由根与系数的关系: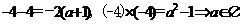 ;
;
当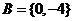 时,由根与系数的关系:
时,由根与系数的关系: ;
;
综上所得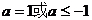 .
.
16. 解法一: (Ⅰ)由图象可知,在(-∞,1)上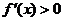 ,在(1,2)上
,在(1,2)上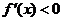 ,在
,在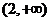 上
上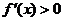 , 故
, 故 在
在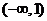 ,
,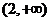 上递增,在(1,2)上递减,因此
上递增,在(1,2)上递减,因此 在
在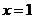 处取得极大值,所以
处取得极大值,所以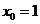 .
.
(Ⅱ)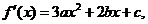 由
由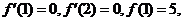 得
得 解得
解得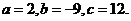
解法二:(Ⅰ)同解法一.
(Ⅱ)设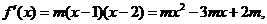
又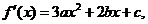 所以
所以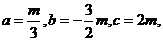
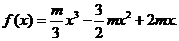
由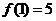 ,即
,即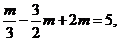 得
得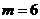 ,
所以
,
所以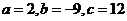 .
.
17. 解:(1) 当 时,
时, ,
,
则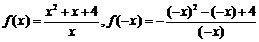
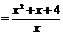
∴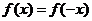 当
当 时,
时,  ,
,
则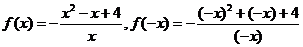
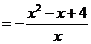 ,
,
∴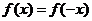
综上所述, 对于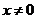 , 都有
, 都有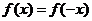 ,∴ 函数
,∴ 函数 是偶函数。
是偶函数。
(2)当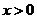 时,
时, 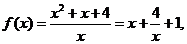
设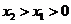 , 则
, 则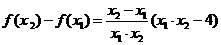 .
.
当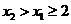 时,
时, 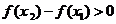 ;
;
当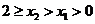 时,
时, 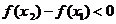 ,
,
∴ 函数 在
在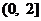 上是减函数, 函数
上是减函数, 函数 在
在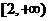 上是增函数。
上是增函数。
(3)由(2)知, 当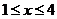 时,
时, 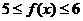 ,
,
又由(1)知, 函数 是偶函数, ∴ 当
是偶函数, ∴ 当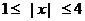 时,
时, 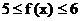 ,
,
∴若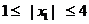 ,
,  , 则
, 则 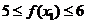 ,
, 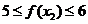 ,
,
∴ , 即
, 即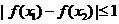 .
.
18.解:(1)因为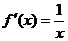 ,所以
,所以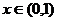 时,
时,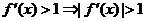 ,
,
即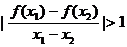 . 当
. 当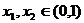 时,
时, ;
;
(2)由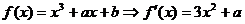 ,
,
当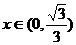 时,
时,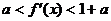 ,因为
,因为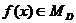 ,
,
所以 ,即
,即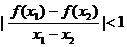 ;
;
所以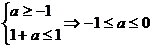 即为所求.
即为所求.
评析:本题应用常规解法,解答较为繁琐;若用导数的几何意义,则十分简单。
19. 解:(1)设方案甲与方案乙的用水量分别为x与z,由题设有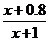 =0.99,解得x=19.
=0.99,解得x=19.
由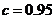 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程:
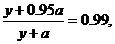 解得y=4
解得y=4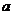 ,故z=4
,故z=4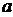 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4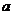 +3.
+3.
因为当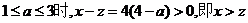 ,故方案乙的用水量较少.
,故方案乙的用水量较少.
(2)设初次与第二次清洗的用水量分别为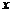 与
与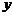 ,类似(I)得
,类似(I)得
 ,
,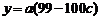 (*)
(*)
于是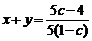 +
+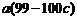

当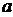 为定值时,
为定值时,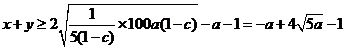 ,
,
当且仅当 时等号成立.此时
时等号成立.此时
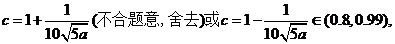
将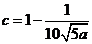 代入(*)式得
代入(*)式得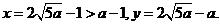
故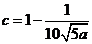 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为
 , 最少总用水量是
, 最少总用水量是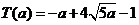 .
.
当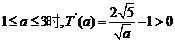 ,故T(
,故T(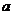 )是增函数(也可以用二次函数的单
)是增函数(也可以用二次函数的单
调性判断).这说明,随着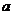 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
20. 解:(Ⅰ)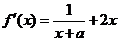 ,依题意有
,依题意有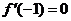 ,故
,故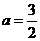 .
.
从而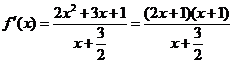 .
.
 的定义域为
的定义域为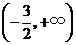 ,当
,当 时,
时,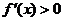 ;
;
当 时,
时,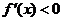 ;当
;当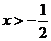 时,
时,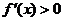 .
.
从而, 分别在区间
分别在区间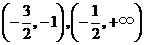 单调增加,在区间
单调增加,在区间 单调减少.
单调减少.
(Ⅱ) 的定义域为
的定义域为 ,
,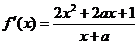 .
.
方程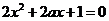 的判别式
的判别式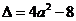 .
.
(ⅰ)若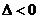 ,即
,即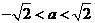 ,在
,在 的定义域内
的定义域内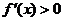 ,故
,故 的极值.
的极值.
(ⅱ)若 ,则
,则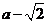 或
或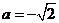 .
.
若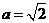 ,
,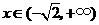 ,
,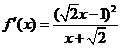 .
.
当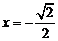 时,
时,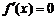 ,当
,当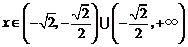 时,
时,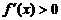 ,所以
,所以 无极值.
无极值.
若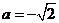 ,
,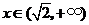 ,
,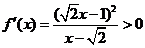 ,
, 也无极值.
也无极值.
(ⅲ)若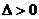 ,即
,即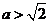 或
或 ,则
,则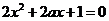 有两个不同的实根
有两个不同的实根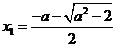 ,
,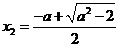 .
.
当 时,
时,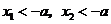 ,从而
,从而 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当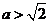 时,
时,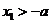 ,
,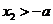 ,
, 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在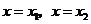 取得极值.
取得极值.
综上, 存在极值时,
存在极值时,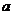 的取值范围为
的取值范围为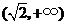 .
.
 的极值之和为
的极值之和为
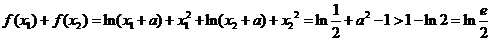 .
.