
保密★启用前【考试时间:2007年11月1日下午3:00―5;00】
四川省绵阳市高中2007级第一次诊断性考试
数 学(理工类)
本试卷分试题卷和答题卷两部分。第1卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。全卷共150分。第1卷答案涂在答题卡上,第Ⅱ卷答案写在答题卷上。
第Ⅰ卷(选择题,共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用4B或5B铅笔填写在答题卡上。
2.每小题选出答案后,用4B或5B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答萎,不能答在试卷上。
3.参考公式:
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B);
如果事件A、B相互独立,那么 P(A?B)=P(A)? P(B);
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率:Pn(k)=?Pk?(1-P)n-k
正棱锥、圆锥的侧面积公式: 锥侧=
锥侧=
球的体积公式V=πR3其中R表示球 的半径
对数换底公式: 0<a
,m ≠ 1,N > 0
0<a
,m ≠ 1,N > 0
 一、选择题:本大题共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上。
一、选择题:本大题共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上。
1.右图中阴影部分表示的集合是
A.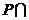
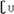
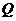 B.
B.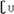
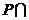
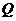
C.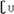 (
(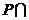
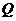 ) D.
) D.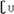 (
(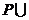
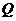 )
)
2.用反证法证明命题:若P则q ,其第一步是反设命题的结论不成立,这个正确的反设是
A.若P则非q B.若非P则q C.非P D.非q
3.已知数列{an}的通项公式为 则{an}的最大项是
则{an}的最大项是
A.a1 B.a2 C.a3 D.a4
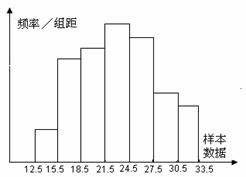 4.右图是一个样本容量为50的样本频率分布直方图,据此估计数据落在[15.5,24.5]的概率约为
4.右图是一个样本容量为50的样本频率分布直方图,据此估计数据落在[15.5,24.5]的概率约为
A.36%
B.46%
C.56%
D.66%
5.在点 x = a 处连续的是

6.设a> 0,a≠ 1,若y = ax的反函数的图象经过点 ,则a=
,则a=
A.16 B.2 C.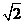 D.4
D.4
7.若函数f(x)的图象经过点 A 、(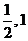 ) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
A. B.
B.
C.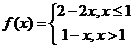 D.
D.
8.计算: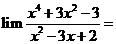
A.不存在 B.8 C.-8 D.18
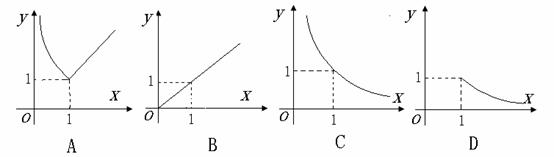
9.函数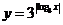 的图象大致是
的图象大致是
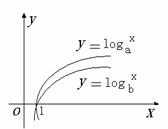
10.对数函数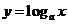 和
和 的图象如图所示,则a 、b的取值范围是
的图象如图所示,则a 、b的取值范围是
 A.
A.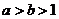
B.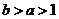
C.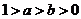
D.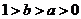
11.已知复数 z ,条件P:“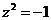 ”是条件q:“
”是条件q:“ 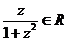 ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
12.函数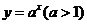 及其反函数的图象与函数
及其反函数的图象与函数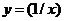 的图象交于A、B两点,若
的图象交于A、B两点,若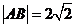 ,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈
0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 )
,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈
0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 )
A.3.8 B.4.8 C.8.4 D.9.2
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡相应位置上。
13.写出一个解集为{xㄏ- 6< x < 1 }且形如ㄏax + bㄏ< c 的绝对值不等式 。
14.化简: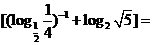 _____________
_____________
15.某路段检查站监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如下的频率分布直方图,则估计在这一时段内通过该站的汽车中车速度不小于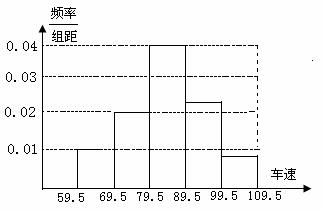 取整数)。
取整数)。
16.若存在正实数x ,使不等式 恒成立,则实数k的取值范围是 。
恒成立,则实数k的取值范围是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
解不等式: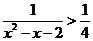
18.(本小题满分12分)
设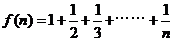 ,用数学归纳法证明:
,用数学归纳法证明: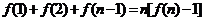 (
(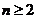 且
且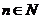 )
)
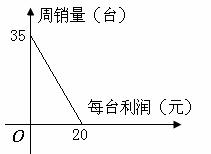 19.(本小题满分12分)商品营销中,商品的质量与它的利润直接相关。某电器商店发现某种型号的函数计数器的周销售量与每台的利润间的一次函数关系如图所示。问:周销售量为多少时,可使商店获得的利润最大?(结果精确到 0.1)。
19.(本小题满分12分)商品营销中,商品的质量与它的利润直接相关。某电器商店发现某种型号的函数计数器的周销售量与每台的利润间的一次函数关系如图所示。问:周销售量为多少时,可使商店获得的利润最大?(结果精确到 0.1)。
20.(本小题满分12分)
有甲、乙两种棉花,从中各抽取等量的样品进行检验,结果如下(其中ξ表示纤维长度,单位:nm )
ξ甲
28
29
30
31
32
P
0.14
a
0.36
0.18
0.14
ξ乙
28
29
30
31
32
P
0.12
0.2
b
0.2
0.12
(1) 求a、b的值;
(2) 计算ξ甲 、 ξ乙 的期望与方差,并说明甲、乙两种棉花的质量情况。
21.(本小题满分12分)
 在△ABC中,∠C = 90o ,BC
= 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF = y ,
在△ABC中,∠C = 90o ,BC
= 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF = y ,
(1)求y与x的函数关系式;
(2)正方形EFGH的面积是否有最大值?试证明你的结论。
22.(本小题满分14分)
已知函数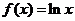
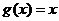
(1)若干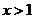 ,求证:
,求证: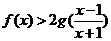
(2)是否存在实数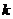 ,是方程
,是方程 有四个不同的实根?若存在,求出
有四个不同的实根?若存在,求出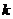 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
一、选择题:本答题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上。
1.A
2.D 对“若 则
则 ”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题;
”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题; 且非
且非 ,即反设命题的结论不成立为非
,即反设命题的结论不成立为非 ,选D。
,选D。
3.B 因为 ,所以,当
,所以,当 时,分母
时,分母 最小,从而
最小,从而 最大为2,选B。
最大为2,选B。
4.C
5.B 设等差数列 的前三项为
的前三项为 (其中
(其中 ),则
),则
 于是它的首项是2,选B
于是它的首项是2,选B
6.D 因为 的反函数的图像经过点
的反函数的图像经过点 ,所以函数
,所以函数 的图像经过点
的图像经过点 ,于是
,于是 ,解得
,解得 ,选D
,选D
7.D 在直角坐标系中较准确地作出点A、B、C,并结合代值验证,可知A、C两点的坐标不满足选择支D的解析式,选D。
8.C 因为分母的极限为零,不能直接使用商的极限运算法则,但这里分子的极限也是零,分子、分母极限之所以为零,就式因为分子、分母都包含有 的因子,先把零因式消去,然后再求极限,得
的因子,先把零因式消去,然后再求极限,得
 ,选C。
,选C。
9.A 函数的定义域为(0,+ ),当
),当 ≥1时,
≥1时, ≥0,有
≥0,有 ;当
;当 时,
时, ,有
,有 ,选A。
,选A。
10.B 根据图像可知,当 时,函数图像从左到右是上升的,表明对数函数是增函数,∴a、b均大于1,排除C、D。于是取
时,函数图像从左到右是上升的,表明对数函数是增函数,∴a、b均大于1,排除C、D。于是取 =2,得
=2,得 ,有
,有

 ,选B.
,选B.
11.A 由 可得
可得 和
和 。容易验证
。容易验证 ,即
,即 。而满足条件
。而满足条件 :“
:“ ”的附属
”的附属 不一定满足条件
不一定满足条件 :“
:“ ”,比如取
”,比如取 ,即
,即 。选A.
。选A.
12.C 设 ,则B
,则B ,有
,有

 ,∴
,∴ 。由于A、B两点在函数
。由于A、B两点在函数 的图象上,则
的图象上,则 =1,∴
=1,∴ ,而点A又在函数
,而点A又在函数 的图像上,∴
的图像上,∴ ,得
,得 ,有
,有 ,于是
,于是 ,选C。
,选C。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13. 或
或 等。
等。
14.原式= 。
。
15.由图知车速小于
16.原不等式等价于 ,令
,令 ,则
,则 ,当
,当 时,
时, ,当
,当 时,
时, 。故
。故
∴ ,∴
,∴ 。
。
三、解答题:本答题共6小题,共74分,解答应写出文字说明、证明过程或验算步骤。
17.(本题满分12分)
解法一 原不等式等价于
 或
或
………………12分
解法二 原不等式等价于
 或
或
 或
或
说明 本题是教材第一册上 页习题1.5第5题:解不等式
页习题1.5第5题:解不等式 的改变,这是关于
的改变,这是关于 的二次双连不等式,若转化为两个二次不等式组成的不等式组来解时,只要善于正确因式分解,数轴标根,也能快速解决。
的二次双连不等式,若转化为两个二次不等式组成的不等式组来解时,只要善于正确因式分解,数轴标根,也能快速解决。
18.(本题满分12分)
(1)当 时,等式左边=
时,等式左边= ,右边=
,右边= ,所以对n=2时,等式成立。………………2分
,所以对n=2时,等式成立。………………2分
(2)假设当 时,等式成立,即
时,等式成立,即 ,则对n=k+1时,
,则对n=k+1时, ,而
,而 )=
)= =
= =
= ,表明
,表明 时,等式成立。
………………10分
时,等式成立。
………………10分
由(1),(2)可知对一切 的自然数等式都成立。
…………12分
的自然数等式都成立。
…………12分
19.(本题满分12分)
设 表示每台的利润,y表示周销售量,则
表示每台的利润,y表示周销售量,则 经过了点(20,0),(0,35),
经过了点(20,0),(0,35),
∴ 解得
解得 ………………4分
………………4分
即 或
或 ,其中
,其中
因此,商店一周中所获利润总额为:
每台利润×销售量=
= ………8分
………8分
由于y是正整数,所以当周销售量为y=17或18时,利润总额最大,为 元,此时
元,此时 元或10.3元。
………………12分
元或10.3元。
………………12分
20.(本小题满分12分)
(1)由 得a=0.18,
得a=0.18, 得b=0.36
………………4分
得b=0.36
………………4分
(2)甲种棉花纤维长度的期望为
 甲 =28×0.14+29×0.18+30×0.36+31×0.18+32×0.14=30
甲 =28×0.14+29×0.18+30×0.36+31×0.18+32×0.14=30
 乙 =28×0.12+29×0.2+30×0.36+31×0.2+32×0.14=30
………8分
乙 =28×0.12+29×0.2+30×0.36+31×0.2+32×0.14=30
………8分
 甲=
甲=

 乙=
乙=
 由于
由于 甲>
甲> 乙,即乙种棉花纤维长度的方差小些,所以乙种棉花的质量较好些(纤维长度比较均匀)………………12分
乙,即乙种棉花纤维长度的方差小些,所以乙种棉花的质量较好些(纤维长度比较均匀)………………12分
说明:本题是选修教材17页8题的改编。
21.(本题满分12分)
(1)延长FE与AB交于点P,则
∵EP//BC,∴ ∽
∽ ,
,
∴ ,即
,即 ,∴
,∴ ,
…………2分
,
…………2分
在直角三角形AEP中, ,
, ,
, ,
,
由勾股定理,得 (*)
(*)
即 。
………………6分
。
………………6分
∵ ∴(*)式成立的充要条件是
∴(*)式成立的充要条件是 ,
,
所以y与x的函数关系式为 , ……8分
, ……8分
(2)因为 ,等号当且仅当
,等号当且仅当 ,即
,即 时取得,
………10分
时取得,
………10分
所以正方形 的面积
的面积 当
当 时取得最大值
时取得最大值 ………12分
………12分
若由 得
得 ,
,
所以 即
即 ,
,
等式右端分子有理化,得
∴ ∵
∵ ∴
∴ ,
,
整理,得 与
与 的函数关系式为
的函数关系式为 (
( )
)
22.(本题满分14分)
(1)令 ,
,
则 ……3分
……3分
因 ,∴
,∴ ,故函数
,故函数 在
在 上是增函数。
上是增函数。
又 在
在 处连续,所以,函数
处连续,所以,函数 在
在 上是增函数。
上是增函数。
∴ 时,
时, 即
即 ………………6分
………………6分
(2)令 ……8分
……8分
则
令 ,则
,则 ,-1,1。
…10分
,-1,1。
…10分
当x变化时, 、
、 的变化关系如下表:
的变化关系如下表:



(―1,0)
0
(0,1)
1


―
0
+
0
―
0
+


极小值

极大值0

极小值

据此可画出 的简图如下,…………12分
的简图如下,…………12分
 故存在
故存在 ,使原方程有4各不同实根。………………14分
,使原方程有4各不同实根。………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com