
2009届高考数学第三轮复习精编模拟十一
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、已知映射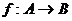 ,其中A=B=R,对应法则
,其中A=B=R,对应法则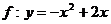 ,对于实数
,对于实数 ,在集合A中不存在原象,则
,在集合A中不存在原象,则 的取值范围是
( )w.w.w.k.s.5.u.c.o.m
的取值范围是
( )w.w.w.k.s.5.u.c.o.m
A.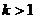 B.
B.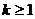 C.
C. 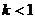 D.
D.
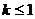
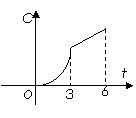
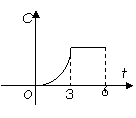
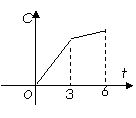
2、某工厂六年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量保持不变,则该厂六年来这种产品的可用图像表示的是 w.w.w.k.s.5.u.c.o.m( )

 |
 |
 |
 |
A. B
 C.
D.
C.
D.
3、已知函数f(x) =3 - 2|x|,g(x) = x2- 2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x) = g(x);当f(x)<g(x)时,F(x) =f(x),那么F(x) ( )
A.有最大值3,最小值-1 B.有最大值3,无最小值
C.有最大值7-2,无最小值 D.无最大值,也无最小值
4、记二项式(1+2x)n展开式的各项系数和为an,其二项式系数和为bn,则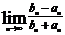 等于 ( )
等于 ( )
A.1 B.-
5、椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点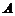 、
、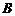 是它的焦点,长轴长为
是它的焦点,长轴长为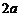 ,焦距为
,焦距为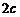 ,静放在点
,静放在点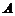 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点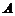 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点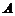 时,小球经过的路程是
( )
时,小球经过的路程是
( )
A.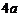 B.
B.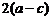 C.
C.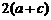 D.以上答案均有可能
D.以上答案均有可能
6、国际上通常用恩格尔系数来衡量一个国家和地区人民生活水平状况,它的计算公式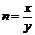 (x:人均食品支出总额,y:人均个人消费支出总额),且
(x:人均食品支出总额,y:人均个人消费支出总额),且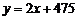 ,各种类型家庭:
,各种类型家庭:
家庭类型
贫困
温饱
小康
富裕
n
n≥59%
50%≤n<59%
40%≤n<50%
30%≤n<40%
李先生居住地2002年比98年食品价格下降了7.5%,该家庭在2002年购买食品和98年完全相同的情况下人均少支出75元,则该家庭2002年属于 ( )
(A ) 贫困 ( B) 温饱 ( C) 小康 (D ) 富裕
7、设0<x<π,则函数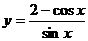 的最小值是
( )
的最小值是
( )
A.3
B.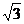 D.2-
D.2-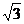
8、函数 的图像关于原点中心对称,则
的图像关于原点中心对称,则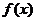 ( )
( )
A.在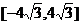 上为增函数 B.在
上为增函数 B.在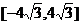 上为减函数
上为减函数
C.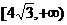 上为增函数,在
上为增函数,在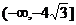 上为减函数
上为减函数
D.在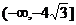 上为增函数,在
上为增函数,在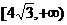 上也为增函数
上也为增函数
9、若集合A1、A2满足A1∪A2=A,则称(A1,A2)为集合A的一个分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分拆,则集合A={a1,a2,a3}?的不同分拆种数是 ( )
A.27
B
10、四面体的顶点和各棱的中点共10个点,在其中取4个点,则这四个点不共面的概
率为 ( )
A、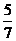 B、
B、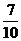 C、
C、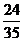 D、
D、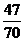
 第二部分 非选择题(共100分)
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、右图是某保险公司提供的资料,在1万元以上的保险单中,有
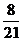 少于2.5万元,那么不少于2.5万元的保险单有
万元.
少于2.5万元,那么不少于2.5万元的保险单有
万元.
12、定义符号函数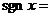
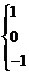
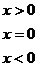 , 则不等式:
, 则不等式: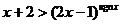 的解集是
.
的解集是
.
13、给出下列8种图像变换方法:
①将图像上所有点的横坐标缩短为原来的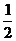 (纵坐标不变);
(纵坐标不变);
②将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变);
③将图像上移1个单位;
④将图像下移1个单位;
⑤将图像向左平移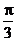 个单位;
个单位;
⑥将图像向右平移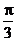 个单位;
个单位;
⑦将图像向左平移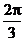 个单位;
个单位;
⑧将图像向右平移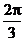 个单位.
个单位.
须且只须用上述的3种变换即可由函数y=sinx的图像得到函数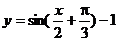 的图像,写出所有的符合条件的答案为 .
的图像,写出所有的符合条件的答案为 .
14、(坐标系与参数方程选做题) 已知抛物线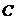 :
: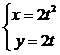 ,(
,(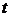 为参数)设
为参数)设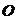 为坐标原点,点
为坐标原点,点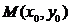 在
在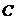 上运动,点
上运动,点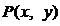 是线段
是线段 的中点,则点
的中点,则点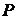 的轨迹普通方程为
的轨迹普通方程为
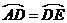 ,
,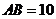 ,
,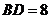 ,则
,则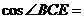 .
.
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16、(本小题满分12分)
已知向量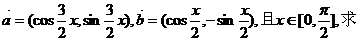
①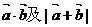 ;
;
②若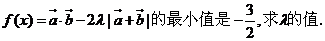
17、(本小题满分12分)
同时抛掷15枚均匀的硬币一次
(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?
请说明理由.
18、(本小题满分14分)
规定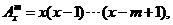 其中
其中 ,
,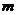 为正整数,且
为正整数,且 这是排列数
这是排列数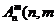 是正整数,且
是正整数,且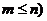 的一种推广.
的一种推广.
(Ⅰ)求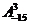 的值;
的值;
(Ⅱ)排列数的两个性质:①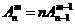 , ②
, ②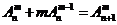 .(其中m,n是正整数)是否都能推广到
.(其中m,n是正整数)是否都能推广到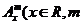 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)确定函数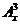 的单调区间.
的单调区间.
19、(本小题满分14分)
如图直角梯形OABC中, ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求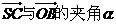 的大小(用反三角函数表示);
的大小(用反三角函数表示);
|