
江苏省2009届高考数学精编模拟试题(一)
一.填空题
1.已知 为虚数单位,则
为虚数单位,则 。
。
2.设集合 =
。
=
。
3.已知等比数列 =
。
=
。
4.图1所示程序框图运行后输出的结果为 。
5.图2是一个空间几何体的三视图,这个几何体的体积是 。
6.已知实数 则“
则“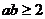 ”是“
”是“ ”的
条件。
”的
条件。
7.已知函数 两函数的图像的交点个数为
。
两函数的图像的交点个数为
。
8.在△ABC中,a,b,c是角A,B,C的对边,若a,b,c成等比数列, 。
。
9. .已知实数 的最小值为
的最小值为
10..已知抛物线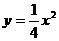 ,过焦点且垂直于对称轴的直线与抛物线交于A,B两个点,则坐标原点与A、B两点构成的三角形的面积为
。
,过焦点且垂直于对称轴的直线与抛物线交于A,B两个点,则坐标原点与A、B两点构成的三角形的面积为
。
情况,采用分层抽样的方法抽取了500户
家庭的月平均电用量,并根据这500户家
庭月平均用量画出频率分布直方图(如图),
则该地区1000户家庭中月平均用电度数
在[70,80]的家庭有 户。
12. .设动直线 与函数
与函数 和
和 的图象分别交于
的图象分别交于 、
、 两点,则
两点,则 的最大值为
.
的最大值为
.
13. 函数
 的最小值是
.
的最小值是
.
14.已知一容器中有A、B两种菌,且在任何时刻A、B两种菌的个数乘积为定值1010。为了简单起见,科学家用 来记录A菌个数的资料,其中
来记录A菌个数的资料,其中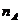 为A菌的个数。则下列判断中正确的个数为
个。
为A菌的个数。则下列判断中正确的个数为
个。
①
②若今天的 值比明天的
值比明天的 值增加1,则今天的A菌个数比昨天的A菌个数多了10个
值增加1,则今天的A菌个数比昨天的A菌个数多了10个
③假设科学家将B菌的个数控制为5万个,则此时5< <5.5
<5.5
二.解答题
15. 在 中,
中,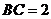 ,
,
 .
.
(Ⅰ)求 ;
;
(11)设 的外心为
的外心为 ,若
,若 ,求
,求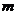 ,
, 的值.
的值.
16.如图,在长方体 中,
中, 分别是
分别是 的中点,M、N分别是
的中点,M、N分别是
(1)求证: 面
面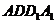
(2)求三棱锥 的体积
的体积
17. 某种家用电器每台的销售利润与该电器的无故障使用时间 (单位:年)有关。若
(单位:年)有关。若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为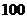 元;若
元;若 ,则销售利润为
,则销售利润为 元.设每台该种电器的无故障使用时间
元.设每台该种电器的无故障使用时间 ,
, 及
及 这三种情况发生的概率分别为
这三种情况发生的概率分别为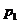 ,
, ,
, ,叉知
,叉知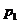 ,
, 是方程
是方程 的两个根,且
的两个根,且
(1)求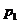 ,
, ,
, 的值;
的值;
(2)记 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 的期望.
的期望.
18. 已知两点 和
和 分别在直线
分别在直线 和
和
 上运动,且
上运动,且 ,动点
,动点 满足:
满足: (
( 为坐标原点),点
为坐标原点),点 的轨迹记为曲线
的轨迹记为曲线 .
.
(Ⅰ)求曲线 的方程,并讨论曲线
的方程,并讨论曲线 的类型;
的类型;
(Ⅱ)过点 作直线
作直线 与曲线
与曲线 交于不同的两点
交于不同的两点 、
、 ,若对于任意
,若对于任意 ,都有
,都有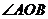 为锐角,求直线
为锐角,求直线 的斜率
的斜率 的取值范围.
的取值范围.
19. 已知函数 .
.
(Ⅰ)求函数 的单调区间及其极值;
的单调区间及其极值;
(Ⅱ)证明:对一切 ,都有
,都有 成立.
成立.
20 在数列
在数列 中,
中, ,且
,且
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令
 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小;
的大小;
(Ⅲ)令
 ,数列
,数列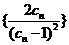 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 都有
都有
试题答案
一.填空题
1. 2.
2.  3.
3.  4. 45
5.
4. 45
5.  6. 充分不必要条件
6. 充分不必要条件
7. 3 8.  9.―3 10.
2 11.1200 12.
3 13. 1 14.1
9.―3 10.
2 11.1200 12.
3 13. 1 14.1
二.解答题
15.
解: (Ⅰ)由余弦定理知:
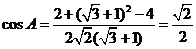 ,
,
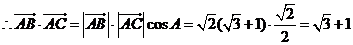 .
.
(Ⅱ)由 ,
,
知



 为
为 的外心,
的外心,
 .
.
同理 .
.
即 ,
解得:
,
解得:
16. (1)证明:取PE中点F,连结MF、NF

MN 面MNF
面MNF
所以MN||面
(2)过D作 的垂线,垂足为G
的垂线,垂足为G
∵BC⊥面 ∴BC⊥DG
∴BC⊥DG
∴DG⊥面PNE
∴
17. 解:(1)由已知得 ,∵
,∵ ,∴
,∴
∵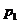 、
、 是方程
是方程 的两个根,∴
的两个根,∴
∴ ,
,
(2) 的可能取值为0,100,200,300,400
的可能取值为0,100,200,300,400
 ,
, ,
,
 ,
, ,
,

即 的分布列为:
的分布列为:


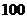









故

 18.解
18.解
(I)由 ,得
,得 是
是 的中点.
的中点.
设 依题意得:
依题意得:

消去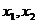 ,整理得
,整理得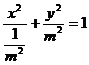 .
.
当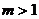 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示圆.
时,方程表示圆.
(II)由 ,焦点在
,焦点在 轴上的椭圆,直线
轴上的椭圆,直线 与曲线
与曲线 恒有两交点,
恒有两交点,
直线斜率不存在时不符合题意;
可设直线 的方程为
的方程为 ,直线与椭圆交点
,直线与椭圆交点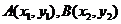 .
.


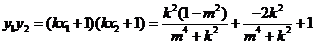 .
.
要使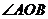 为锐角,只需
为锐角,只需
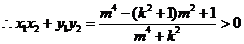 .
.
即 ,
,
可得 ,对于任意
,对于任意 恒成立.
恒成立.
而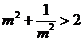 ,
,
所以 的取值范围是
的取值范围是 .
.
19. (Ⅰ)解: ,令
,令 ,得
,得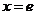 .
.






0


增
极大值
减
由上图表知:
 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.
 的极大值为
的极大值为 .
.
(Ⅱ)证明:对一切 ,都有
,都有 成立
成立
则有
由(Ⅰ)知, 的最大值为
的最大值为 ,并且
,并且 成立,当且仅当
成立,当且仅当 时成立,
时成立,
函数 的最小值大于等于函数
的最小值大于等于函数 的最大值,但等号不能同时成立.
的最大值,但等号不能同时成立.
所以,对一切 ,都有
,都有 成立.
成立.
20. 解:(Ⅰ) ,
,
 ,
,
即 (
(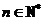 ).
).
(II) ,
,
 .
.
猜想当 时,
时, .
.
下面用数学归纳法证明:
①当 时,由上可知
时,由上可知 成立;
成立;
②假设 时,上式成立,即
时,上式成立,即 .
.
当 时,
时,

所以当 时成立.
时成立.
由①②可知当
 时,
时, .
.
综上所述当 时,
时,  ;
;
当 时,
时,  ;
;
当
 时,
时, .
.
(III)
当 时,
时,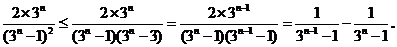
所以
+ .
.
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com