
2007年南通市高三第一次调研考试
数学试题
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则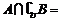
A.{4,5} B.{2,3} C.{1} D.{2}
2.
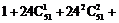 …
…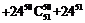 除以9的余数是
除以9的余数是
A.1
B.
3.
函数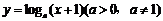 的定义域和值域均为[0,1],则a等于
的定义域和值域均为[0,1],则a等于
A. B.
B. D.
D.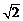
4. 双曲线的一条渐近线与实轴的夹角为α,则双曲线的离心率为
A.sinα B.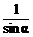 C.cosα D.
C.cosα D.
5. 对某种电子元件使用寿命跟踪调查,所得样本频率分布直方图如右图,由图可知一批电子元件中寿命在100~300小时的电子元件的数量与寿命在300~600小时的电子元件的数量的比是
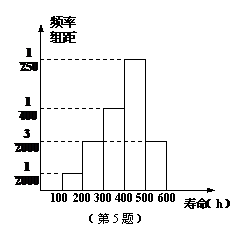 A.
A. B.
B.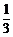
C. D.
D.
6. 函数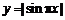 的单调递增区间是
的单调递增区间是
A.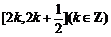
B.
C.
D.
7. 箱内有大小相同的6个红球和4个黑球,从中每次取1个球记下颜色后再放回箱中,则前3次恰有1次取到黑球的概率为
A. B.
B. C.
C. D.
D.
8. 空间四条直线a,b,c,d,满足a⊥b,b⊥c,c⊥d,d⊥a,则必有
A.a⊥c B.b⊥d C.b∥d 或a∥c D.b∥d 且a∥c
9. 若a>0,b>0,a3+b3< 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.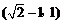
10.△ABC的外接圆圆心为O,且 ,则∠C等于
,则∠C等于
A.45° B.60° C.75° D.90°
二、填空题:本大题共6小题,每小题5分,共30分.把答案填写在答题卡相应位置上.
11.已知向量a=(-1,1),b= ,则a与b的夹角α= ▲ .
,则a与b的夹角α= ▲ .
12.垂直于直线x-3y=0且与曲线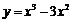 相切的直线方程为 ▲ .
相切的直线方程为 ▲ .
13.椭圆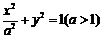 的一个焦点为F,点P在椭圆上,且
的一个焦点为F,点P在椭圆上,且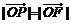 (O为坐标原点),则
(O为坐标原点),则
△OPF的面积S= ▲ .
14.数列{an}中,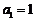 ,
,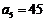 ,且
,且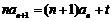 ,则常数t= ▲ .
,则常数t= ▲ .
15.一排7个座位,让甲、乙、丙三人就坐,要求甲与乙之间至少有一个空位,且甲与丙之间也至少有一个空位,则不同的坐法有 ▲ 种.
16.已知函数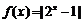 ,当
,当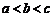 时,有
时,有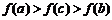 .给出以下命题:
.给出以下命题:
(1)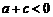 ;(2)
;(2)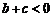 ;(3)
;(3)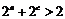 ;(4)
;(4)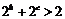 .
.
则所有正确命题的序号是 ▲ .
三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知抛物线的顶点在原点,焦点F在x轴的正半轴上,且过点P(2,2),过F的直线交抛物线于A(x1,y1),B(x2,y2)两点.
(1)求抛物线的方程;
(2)设直线l是抛物线的准线,求证:以AB为直径的圆与直线l相切.
18.(本题满分14分)
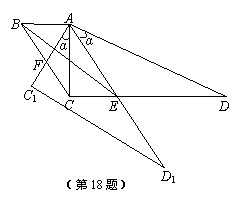 在同一平面内,Rt△ABC和Rt△ACD拼接如图所示,现将△ACD绕A点顺时针旋转α角(0<α<
在同一平面内,Rt△ABC和Rt△ACD拼接如图所示,现将△ACD绕A点顺时针旋转α角(0<α<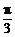 )后得△AC1D1,AD1交DC于点E,AC1交BC于点F.∠BAC=∠ACD=
)后得△AC1D1,AD1交DC于点E,AC1交BC于点F.∠BAC=∠ACD=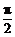 ,∠ACB=∠ADC=
,∠ACB=∠ADC=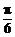 ,AC=
,AC=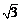 .
.
(1)当AF=1时,求α;
(2)求证:对任意的α∈(0,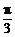 ),
),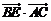 为定值.
为定值.
19.(本题满分14分)
正四棱锥S-ABCD中,O为底面中心,E为SA的中
点,AB=1,直线AD到平面SBC的距离等于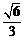 .
.
(1)求斜高SM的长;
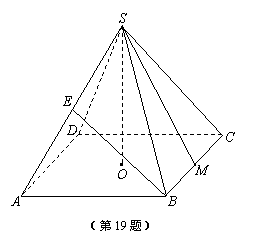 (2)求平面EBC与侧面SAD所成锐二面角的大小;
(2)求平面EBC与侧面SAD所成锐二面角的大小;
(3)在SM上是否存在点P,使得OP⊥平面EBC?
并证明你的结论.
20.(本题满分15分)
(1)设a,n∈N*,a≥2,证明: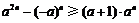 ;
;
(2)等比数列{an}中,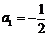 ,前n项的和为An,且A7,A9,A8成等差数列.设
,前n项的和为An,且A7,A9,A8成等差数列.设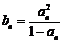 ,数列{bn}前n项的和为Bn,证明:Bn<
,数列{bn}前n项的和为Bn,证明:Bn<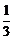 .
.
21.(本题满分15分)
已知函数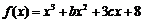 和
和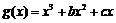 (其中
(其中 ),
),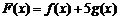 ,
,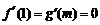 .
.
(1)求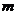 的取值范围;
的取值范围;
(2)方程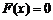 有几个实根?为什么?
有几个实根?为什么?
2007年南通市高三第一次调研考试
1.C 2.A 3.B 4.D 5.C 6.B 7.D 8.C 9.B 10.A
11.120° 12.3x+y-1=0 13. 14.10 15.100 16.(1),(4)
14.10 15.100 16.(1),(4)
17.解:(1)设抛物线 ,将(2,2)代入,得p=1. …………4分
,将(2,2)代入,得p=1. …………4分
∴y2=2x为所求的抛物线的方程.………………………………………………………5分
(2)联立 消去y,得到
消去y,得到 . ………………………………7分
. ………………………………7分
设AB的中点为 ,则
,则 .
.
∴ 点 到准线l的距离
到准线l的距离 .…………………………………9分
.…………………………………9分
而 ,…………………………11分
,…………………………11分
 ,故以AB为直径的圆与准线l相切.…………………… 12分
,故以AB为直径的圆与准线l相切.…………………… 12分
(注:本题第(2)也可用抛物线的定义法证明)
18.解:(1)在△ACF中, ,即
,即 .………………………………5分
.………………………………5分
∴ .又
.又 ,∴
,∴ .……………………
7分
.……………………
7分
(2)


 . ……………………………14分
. ……………………………14分
(注:用坐标法证明,同样给分)
19.
解法一:(1)连OM,作OH⊥SM于H.
∵SM为斜高,∴M为BC的中点,∴BC⊥OM.
∵BC⊥SM,∴BC⊥平面SMO.
又OH⊥SM,∴OH⊥平面SBC.……… 2分
由题意,得 .
.
设SM=x,
则 ,解之
,解之 ,即
,即 .………………… 5分
.………………… 5分
(2)设面EBC∩SD=F,取AD中点N,连SN,设SN∩EF=Q.
 ∵AD∥BC,∴AD∥面BEFC.而面SAD∩面BEFC=EF,∴AD∥EF.
∵AD∥BC,∴AD∥面BEFC.而面SAD∩面BEFC=EF,∴AD∥EF.
又AD⊥SN,AD⊥NM,AD⊥面SMN.
从而EF⊥面SMN,∴EF⊥QS,且EF⊥QM.
∴∠SQM为所求二面角的平面角,记为α.……… 7分
由平几知识,得 .
.
∴ ,∴
,∴ .
.
∴ ,即所求二面角为
,即所求二面角为 . ……………… 10分
. ……………… 10分
(3)存在一点P,使得OP⊥平面EBC.取SD的中点F,连FC,可得梯形EFCB,
取AD的中点G,连SG,GM,得等腰三角形SGM,O为GM的中点,
设SG∩EF=H,则H是EF的中点.
连HM,则HM为平面EFCB与平面SGM的交线.
又∵BC⊥SO,BC⊥GM,∴平面EFCB⊥平面SGM. …………… 12分
在平面SGM中,过O作OQ⊥HM,由两平面垂直的性质,可知OQ⊥平面EFCB.
而OQ 平面SOM,在平面SOM中,延长OQ必与SM相交于一点,
平面SOM,在平面SOM中,延长OQ必与SM相交于一点,
故存在一点P,使得OP⊥平面EBC. ……………………… 14分

|