
2005年上海静安区初三数学学业检测试卷
(100分钟完成, 满分120分)
一、填空题(本题共14小题,每小题3分,满分42分)
1.如果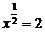 ,那么
,那么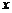 =
.
=
.
2.在实数范围内分解因式: =
.
=
.
3.方程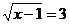 的根是______________.
的根是______________.
4.方程组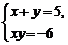 的解是_____________.
的解是_____________.
5.函数y =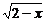 的定义域是_____________.
的定义域是_____________.
6.如果点(2,?3)在反比例函数的图象上,那么这个反比例函数的解析式是__________.
7.写出一个图象不经过第一象限的一次函数:________________.
8.已知函数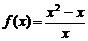 , 如果
, 如果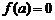 , 那么
, 那么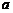 =_________.
=_________.
9. 某单位全体职工中, 月工资在3000元到4000元的人数为150, 频率是0.3, 那么这个单位的职工总人数是______________.
10.如果在△ABC中,AD是中线,G是重心,那么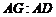 的值为___________.
的值为___________.
11.在△ABC中,点D、E分别在AB、AC边上,如果DE//BC,AD=1,AB=3,DE=2,那么BC =____________.
12.三角形的内心到三角形___________的距离相等.
13.正五边形绕着它的中心最少旋转___________度后与它本身重合.
14.已知l是⊙O的切线,⊙O的直径AB=10cm,那么点A、B到直线l的距离之和为_______cm.
[本题每小题所列出的四个选项中,只有一个是正确的,把正确答案的代号填入括号内]
二、 选择题(本题共4小题,每小题3分,满分12分)
15.下列方程中为无理方程的是…………………………………………………………( )
(A) 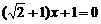 ; (B)
; (B)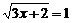 ; (C)
; (C)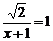 ; (D)
; (D)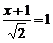 .
.
16.在下列函数中,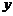 随着
随着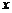 增大而减小的是……………………………………………( )
增大而减小的是……………………………………………( )
(A) 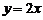 ; (B)
; (B)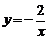 ; (C)
; (C)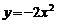 ; (D)
; (D)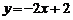 .
.
17.在Rt△ABC中,∠C=90°,那么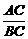 等于……………………………………………( )
等于……………………………………………( )
(A)tgA;
(B)ctgA; (C)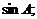 (D)
(D)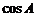 .
.
18.如果两个圆只有一个公共点,那么这两个圆的公切线条数是…………………………( )
(A)1; (B)2; (C)3; (D)1或3.
三、 (本题共3小题,每小题8分,满分24分)
19.解方程: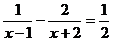 .
.
 20.如图1,在□ABCD中,AB=10,∠B为锐角,sinB=
20.如图1,在□ABCD中,AB=10,∠B为锐角,sinB=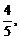 tg∠ACB=
tg∠ACB=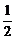 ,求AD、AC长.
,求AD、AC长.
|