
2005年烟台市初中毕业、升学统一考试
第一卷
一、 选择题(本题共12个小题。每小题4分。满分48分)每小题都给出标号为A、B、C、D四个备选答案,其中有且只有一个是正确的.
1.计算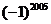 的结果是
的结果是
A.-l B.1 C.-2005 D.2 005
2.已知四个命题:(1)如果一个数的相反数等于它本身,则这个数是0;(2)一个数的倒数等于它本身,则这个数是1;(3)一个数的算术平方根等于它本身,则这个数是1或O;(4)如果一个数的绝对值等于它本身,则这个数是正数.其中真命题有
A.1个 B.2个 C. 3个 D.4个
3.如图,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC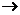 CA
CA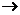 AB
AB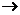 BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体
BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体
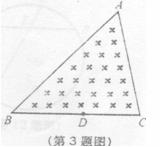
A.转过90° B.转过180° C.转过270° D.转过360°
4.近似数O.09070的有效数字和精确度分别是
A.四个,精确到万分位 B.三个,精确到十万分位
C.四个,精确到十万分位 D.三个,精确到万分位
5.如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC 4cm,则EF的长等于
4cm,则EF的长等于
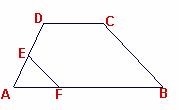
A.1.5cm B.2cm C.2.5cm D.3cm
6.如果等式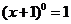 和
和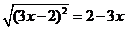 同时成立,那么需要的条件是
同时成立,那么需要的条件是
A. 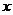 ≠-1 B.
≠-1 B.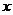 <
<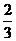 且
且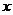 ≠-1 C.
≠-1 C. 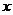 ≤
≤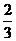 或
或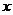 ≠-1 D.
≠-1 D.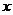 ≤
≤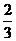 且
且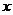 ≠-1
≠-1
7.如图,四边形ABCD内接于⊙O,AB BC.AT是⊙O的切线,∠BAT
BC.AT是⊙O的切线,∠BAT 55°,则∠D等于
55°,则∠D等于
A.110° B.115°
C.120° D.125°
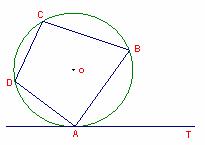 7题图
7题图 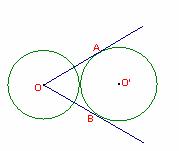 8题图
8题图
8.如图,两个等圆⊙O和⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB等于
A.30° B.45°
C.60° D.75°
9.已知样本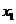 ,
,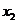 ,…,
,…,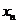 的方差是2,则样本3
的方差是2,则样本3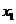 +5,3
+5,3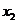 +5,…,3
+5,…,3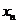 +5的方差是
+5的方差是
A.11 B.18 C.23 D.36(样本的方差)
10.如图,△ABC中,∠ACB 90°,∠B
90°,∠B 30°, AC
30°, AC 1,过点C作
1,过点C作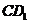 ⊥AB于
⊥AB于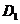 ,过点
,过点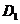 作
作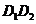 ⊥BC于
⊥BC于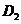 ,过点
,过点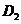 作
作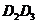 ⊥AB于
⊥AB于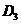 ,这样继续作下 去,线段
,这样继续作下 去,线段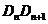 (
(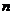 为正整数)等于(直角三角形、相似三角形)
为正整数)等于(直角三角形、相似三角形)
A.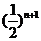 B.
B.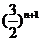 C.
C.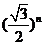 D.
D.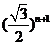
10题图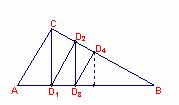
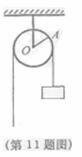
11.一定滑轮的起重装置如图,滑轮半径为12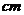 ,当重物上升4π
,当重物上升4π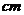 时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动) (圆的弧长)
时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动) (圆的弧长)
A.12° B.30°
C 60° D.90°
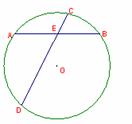
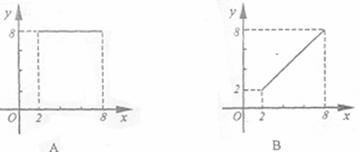
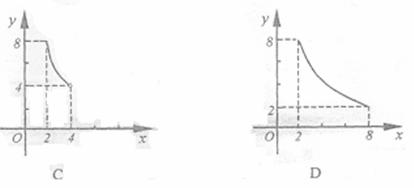
12.如右图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在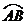 上运动,且不与A、B重合),设EC
上运动,且不与A、B重合),设EC
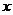 ,ED
,ED y,下列能够表示y与
y,下列能够表示y与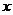 之间函数关系的图象是
之间函数关系的图象是
第 Ⅱ 卷
二、填空题(本题共6个小题,每小题4分,满分24分)
13.写出两个和为1的无理数_____(只写一组即可).
14.如图,两个半径为1,圆心角是90°的扇形OAB和扇 形0′A′B′,叠放在一起,点0′在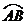 上,四边形OPO′Q是正方形,则阴影部分的面积等__.
上,四边形OPO′Q是正方形,则阴影部分的面积等__.

15.已知方程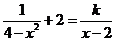 有增根,则
有增根,则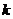
 ___.
___.
16.将一张正方形纸片沿一对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折,把得到的图形(如图)沿虚线剪开,打开阴影部分并铺平,此图形有___条对称轴.
17.已知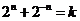 (n为正整数),则
(n为正整数),则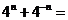 _____(用含
_____(用含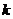 的代数式表示).
的代数式表示).
18.如图,有六个矩形水池环绕.矩形的内侧一边所在直线恰好围成正六边形ABCDEF,正六边形的边长为4米.要从水源点P处向各水池铺设供水管道,这些管道的总长度最短是___米
三、解答题(本大题共8个小题,满分78分.解答题要写出必要的文字说明、证明过程或演算步骤)
19.(本题满分6分)先化葡,再求值:
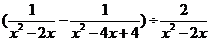 ,其中
,其中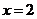
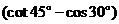
20.(本题满分7分)
视力水平的下降已经引起全社会的关注.某中学为了解初四毕业班学生的视力情况,在今年4月对全体毕业班学生的视力进行了检测,将所得数据整理后画出频率分布直方图(如图),已知图中从左到右第一、第二、第三、第五小组的频率分别为0.05,O.1,O.15,O.1,第第四小组的频数是420. (统计计算)
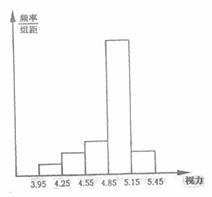
请完成下列填空:
(1)第四小组的频率是___;
(2)今年初四毕业班有___名学生;
(3)如果视力不小于4.9属于正常,那么有___名学生视力正常;
(4)这组数据的中位数在第___小组;
(5)2003年4月检测的该批学生中有640名学生视力正常,那么两年来视力正常学生人数的平均下降率是___.
王老师在黑板上出了这样一道习题:设方程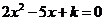 的两个实数根是
的两个实数根是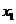 ,
,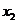 ,请你选取一个适当的
,请你选取一个适当的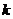 值,求
值,求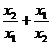 的值.
的值.
小明同学取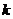 =4,则方程是
=4,则方程是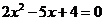 .
.
由根与系数的关系,得: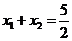 ,
, 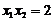 .
.
∴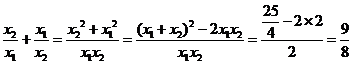
即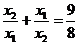 .
.
问题(1):请你对小明解答的正误作出判断,并说明理由.
问题(2):请你另取一个适当的正整数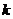 ,其它条件不变,不解方程,改求
,其它条件不变,不解方程,改求 的值.
的值.
22. (本题满分9分)
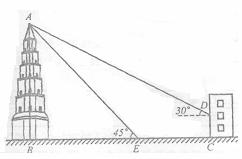
某风景区内有一古塔AB,在塔的北面有一建筑物,冬至日的正午光线与水平面的夹角是30°,此时塔在建筑物的墙上留下了高3米的影子CD;而在春分日正午光线与地面的夹角是45°,此时塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),
求塔AB的高度(结果保留根号).
23.(本题满分10分)
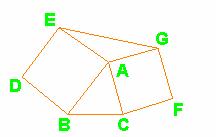
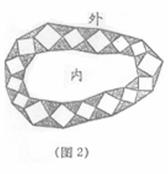
(1)如图1,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,试判断△ABC与△AEG面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是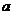 平方米,内圈的所有三角形的面积之和是
平方米,内圈的所有三角形的面积之和是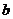 平方米,这条小路一共占地多少平方米?
平方米,这条小路一共占地多少平方米?
24.(本题满分11分)
为庆祝“六一”儿童节,某市中小学统一组织文艺汇演.甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
如果两所学校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两所学校各有多少学生准备参加演出?
(3)如果甲校有lO名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
25.(本题满分12分)
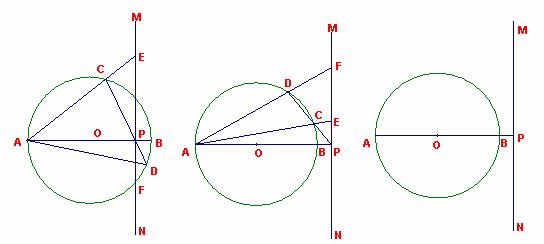
(1)如图1,直线MN与⊙0相交,且与⊙0的直径AB垂直,垂足为P,过点P的直线与⊙0交于C、D两点,直线AC交MN于点E,直线AD交MN于点F.
求证:PC?PD PE?PF.
PE?PF.
(2)如图2,若直线MN与⊙0相离.(1)中的其余条件不变,那么(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)在图3中,直线MN与⊙0相离,且与⊙0的直径AB垂直,垂足为P.①请按要求
画出图形:画⊙0的割线PCD(PC<PD),直线BC与MN交于E,直线BD与MN交于F.②能否仍能得到(1)中的结论?请说明理由.
26.(本题满分14分) (圆、抛物线、直线)
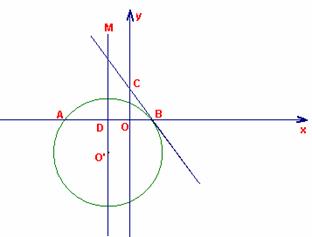
如图,在平面直角坐标系中,以点0′(-2,-3)为圆心,5为半径的圆交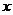 轴于A、B两点,过点B作⊙0′的切线,交
轴于A、B两点,过点B作⊙0′的切线,交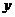 轴于点C,过点0′作
轴于点C,过点0′作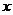 轴的垂线MN,垂足为D,一条抛物线(对称轴与y轴平行)经过A、B两点,且顶点在直线BC上.
轴的垂线MN,垂足为D,一条抛物线(对称轴与y轴平行)经过A、B两点,且顶点在直线BC上.
(1)求直线BC的解析式.
(2)求抛物线的解析式.
(3)设抛物线与y轴交于点P,在抛物线上是否存在一点Q,使四边形DBPQ为平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com