
2005年泰安市中等学校招生考试
第Ⅰ卷
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确
1.倒数是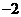 的数是有理数
的数是有理数
(A)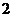 (B)
(B)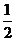
(C)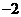 (D)
(D)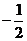
2.若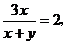 则
则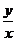 的值为比例的性质
的值为比例的性质
(A)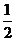 (B)
(B)
(C)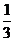 (D)
(D)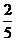
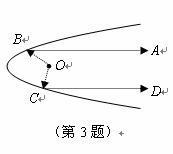
3.探照灯、锅形天线、汽车灯以及其它很多灯具都与抛物线形状 有关,如图所示是一探照灯灯碗的纵剖面,从位于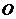 点的灯泡发出的两束光线
点的灯泡发出的两束光线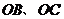 经灯碗反射以后平行射出.如果图中
经灯碗反射以后平行射出.如果图中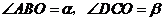 ,则
,则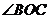 的度数为抛物线的性质
的度数为抛物线的性质
(A)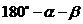 (B)
(B)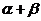
(C)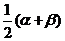 (D)
(D)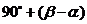
4.两实数根的和是3的一元二次方程为根与系数的关系
(A)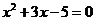 (B)
(B)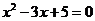
(C)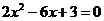 (D)
(D)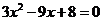
5.一次魔术表演时,桌面上摆放着四张扑克牌.一位观众应邀登台将摩术师的眼睛蒙上黑
布并把其中一张扑克牌旋转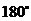 后放回原处,取下黑布后,魔术师立即就指出了哪张
后放回原处,取下黑布后,魔术师立即就指出了哪张
牌被旋转过.下面给出了四组牌,假如你是魔术师,你应该选择哪一组才能达到上述效
果?图形的旋转与对称

 6.若
6.若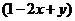 是
是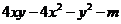 的一个因式,则
的一个因式,则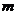 的值为因式分解
的值为因式分解
(A)4 (B)1
(C)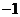 (D)0
(D)0
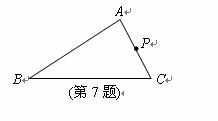
7.如图所示,在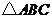 中,
中, 是
是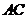 的中点,过
的中点,过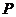 点的直线交
点的直线交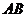 于
于
点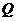 ,若以
,若以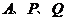 为顶点的三角形和以
为顶点的三角形和以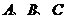 为顶点的三角形相似,则
为顶点的三角形相似,则 的
的
长为相似三角形的性质
(A)3 (B)3或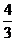
(C)3或 (D)
(D)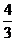
8.抛物线 的对称轴是抛物线的性质
的对称轴是抛物线的性质
(A)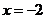 (B)
(B)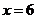
(C)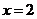 (D)
(D)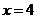
9.某校现有学生1800人,为了增强学生的法律意识,学校组织全体学生进行了一次普法测试.现抽取部分测试成绩(得分取整数)作为样本,进行整理后分成五组,并绘制成频数分布直方图.根据图中提供的信息,下列判断不正确的是数据的收集与处理
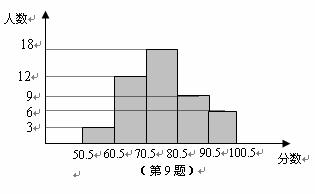
(A)样本容量是48
(B)估计本次测试全校在90分以上的学生约有225人
(C)样本的中位数落在70.5~80.5这一分数段内
(D)样本中50.5~70.5这一分数段的频率是0.25
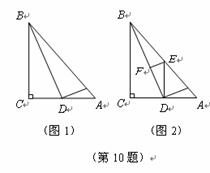
10.直角三角形纸片的两直角边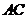 与
与 之比为
之比为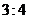 .
.
(1)将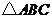 如图1那样折叠,使点
如图1那样折叠,使点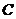 落在
落在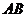 上,折痕为
上,折痕为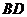 ;
;
(2)将 如图2那样折叠,使点
如图2那样折叠,使点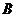 与点
与点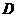 重合,折痕为
重合,折痕为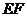 . 则
. 则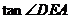 的值为锐角三角函数、轴对称
的值为锐角三角函数、轴对称
(A) (B)
(B)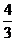 (C)
(C)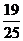 (D)
(D)
11.如图所示,在直角坐标系中, 点坐标为
点坐标为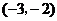 ,⊙A的半径为1,
,⊙A的半径为1,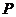 为
为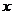 轴上一动点,
轴上一动点, 切⊙A于点
切⊙A于点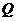 ,则当
,则当 最小时,
最小时,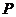 点的坐标为
点的坐标为

(A)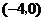 圆与直角坐标系
圆与直角坐标系
(B)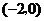
(C) 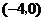 或
或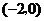
(D)
12.某人才市场2004年上半年应聘和招聘人数排名前5个类别的情况如下图所示,
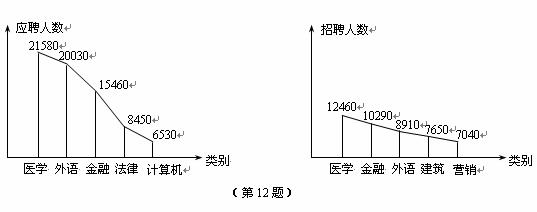 若用同一类别中应聘人数与招聘人数比值的大小来衡量该类别的就业情况,则根据图中
若用同一类别中应聘人数与招聘人数比值的大小来衡量该类别的就业情况,则根据图中
信息,下列对就业形势的判断一定正确的是 统计
(A)医学类好于营销类
(B)金融类好于计算机类
(C)外语类最紧张
(D)建筑类好于法律类
第Ⅱ卷
二、填空题(本题共7小题,满分21分.只要求填写最后结果,每小题填对得3分)
13.当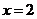 时,代数式
时,代数式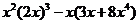 的值是求代数式的值 .
的值是求代数式的值 .
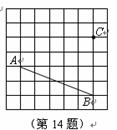
14.如图,已知图中每个小方格的边长均为1,则点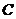 到直线
到直线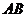 的距离为 (结果保留根号).
的距离为 (结果保留根号).
15.若一个偶数的立方根比2大,平方根比4小,则这个数一定是 .
16.如图所示, ,半径为
,半径为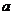 的
的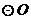 切
切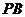 于
于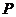 点.若将
点.若将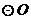 在
在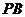 上向右滚动,则当滚动到
上向右滚动,则当滚动到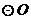 与
与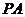 也相切时,圆心
也相切时,圆心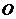 移动的水平距离是 .
移动的水平距离是 .


17.实数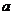 在数轴上的位置如图所示,则化简
在数轴上的位置如图所示,则化简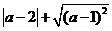 的结果为 .
的结果为 .
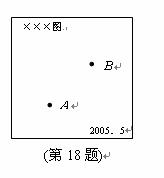
18.在一次中学生野外生存训练活动中,每位队员都配发了一张地图,并接到训练任务:要求36小时之内到达目的地.但是,地图上并未标明目的地的具体位置,仅知道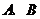 两地坐标分别为
两地坐标分别为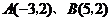 ,且目的地离
,且目的地离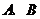 两地的距离分别为
两地的距离分别为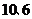 ,如图所示,则目的地确切位置的坐标为 .
,如图所示,则目的地确切位置的坐标为 .
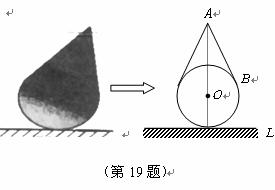
19.用一直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽可以制成一个不倒翁玩具,不倒翁的轴剖面图如右图所示,圆锥的母线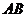 与
与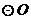 相切于点
相切于点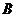 ,不倒翁的顶点
,不倒翁的顶点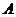 到桌面
到桌面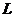 的最大距离是18cm.若将圆锥形纸帽的表面全涂上颜色,则需要涂色部分的面积约为 cm2(精确到1cm2).
的最大距离是18cm.若将圆锥形纸帽的表面全涂上颜色,则需要涂色部分的面积约为 cm2(精确到1cm2).
演步骤)
三、解答题(本大题共7个小题,满分63分,解答应写出必要的文字说明、证明过程或推
20.(7分)
解方程: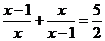 .
.
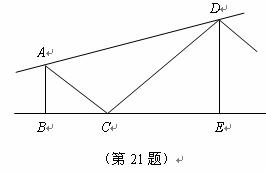
21.(8分)
如图所示是一个钢架结构示意图的一部分,其中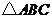 和
和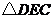 均为等腰直角三角
均为等腰直角三角
形,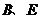 分别为直角顶点.为了增强钢架的牢固性,计划连接
分别为直角顶点.为了增强钢架的牢固性,计划连接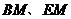 (其中
(其中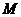 为
为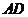 的中点).
的中点).
(1)请用尺规作出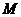 点(保留作图痕迹,不写作法);
点(保留作图痕迹,不写作法);
(2)判断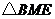 的形状.并证明你的结论.
的形状.并证明你的结论.
22.(9分)
下图是按一定规律排列的方程组集合和它们解的集合的对应关系图:
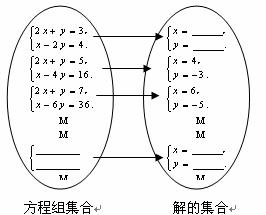
若方程组集合中的方程组自上而下依次记作方程组1、方程组2、方程组3、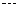 、方程
、方程
组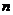 .
.
(1)将方程组1的解填入上图中;
(2)请依据方程组和它的解变化的规律,将方程组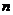 和它的解直接填入集合图中;
和它的解直接填入集合图中;
(3)若方程组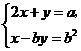 的解是
的解是 ,求
,求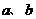 的值;并判断该方程组是否符合(2)中的规律?
的值;并判断该方程组是否符合(2)中的规律?
23.(9分)
某“希望学校”为加强信息技术课教学,拟投资建一个初级计算机房和一个高级计算机房,每个机房只配置1台教师用机,若干台学生用机.现有厂方提供的产品推介单一份,如下表.
现知:教师配置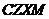 系列机型,学生配置
系列机型,学生配置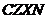 系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
请计算,拟建的两个机房各能配置多少台学生用机?

24.(10分)
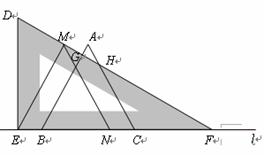
已知,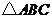 是等边三角形,将一块含
是等边三角形,将一块含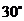 角的直角三角板
角的直角三角板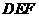 如图放置,让三角板在
如图放置,让三角板在 所在的直线
所在的直线 上向右平移.当点
上向右平移.当点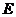 与点
与点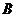 重合时,点
重合时,点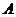 恰好落在三角板的斜边
恰好落在三角板的斜边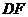 上.
上.
问:在三角板平移过程中,图中是否存在与线段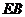 始终相等的线段(假定
始终相等的线段(假定 与三角板斜边的交点为
与三角板斜边的交点为 )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.
)?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.
(说明:结论中不得含有图中未标识的字母)
25.(10分)
水库的库容通常是用水位的高低来预测的.下表是某市一水库在某段水位范围内的库容与水位高低的相关水文资料,请根据表格提供的信息回答问题.
水位高低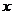 (单位:米)
(单位:米)
10
20
30
40
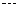
库容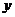 (单位:万立方米)
(单位:万立方米)
3000
3600
4200
4800
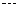
(1)将上表中的各对数据作为坐标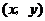 ,在给出的坐标系中用点表示出来:
,在给出的坐标系中用点表示出来:
(2)用线段将(1)中所画的点从左到右顺次连接.若用此图象来模拟库容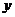 与水位高低
与水位高低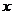 的函数关系.根据图象的变化趋势,猜想
的函数关系.根据图象的变化趋势,猜想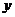 与
与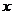 间的函数关系,求出函数关系式并加以验证;
间的函数关系,求出函数关系式并加以验证;
(3)由于邻近市区连降暴雨,河水暴涨,抗洪形势十分严峻,上级要求该水库为其承担部分分洪任务约800万立方米.若该水库当前水位为65米,且最高水位不能超过79米.请根据上述信息预测:该水库能否承担这项任务?并说明理由.

26.(10分)
某“研究性学习小组”遇到了以下问题,请参与:
已知,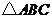 是等边三角形且内接于
是等边三角形且内接于 ,取
,取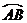 上异于
上异于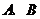 的点
的点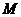 .设直线
.设直线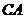 与
与 相交于点
相交于点 ,直线
,直线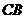 与
与 相交于点
相交于点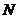 .
.
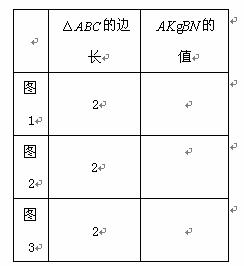
(1)如图1、图2、图3,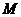 分别为
分别为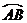 的中点、三分之一点、四分之一点,
的中点、三分之一点、四分之一点,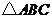 的边长均为2,分别测量出
的边长均为2,分别测量出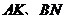 的长,计算
的长,计算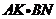 的值(精确到0.01)并将结果填入下表中:
的值(精确到0.01)并将结果填入下表中:

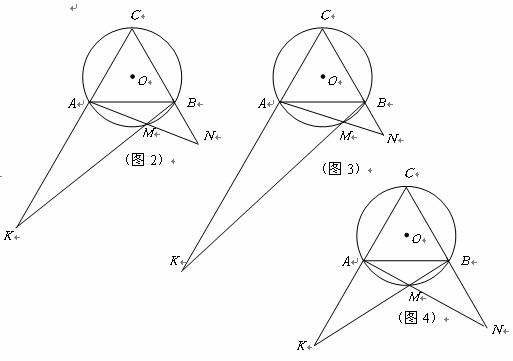
(2)如图4,当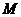 为
为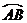 上任意一点时,根据(1)的结果,猜想
上任意一点时,根据(1)的结果,猜想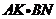 与
与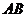 的数量关系式为 ;
的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com