
2006年山东省滨州市中等学校招生统一考试
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把选出的答案字母标号填在第Ⅱ卷前的答题表内,否则不得分.
1.函数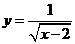 的自变量
的自变量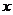 的取值范围是( )
的取值范围是( )
A.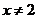 B.
B.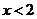 C.
C.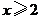 D.
D.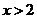
2.下列运算中,正确的是( )
A.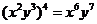 B.
B.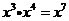
C.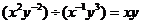 D.
D.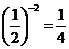
3.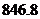 亿度,用科学记数法记作(保留三位有效数字)( )
亿度,用科学记数法记作(保留三位有效数字)( )
A.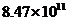 度 B.
度 B.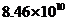 度 C.
度 C.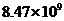 度 D.
度 D.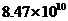 度
度
 4.如图1,在半径为10的
4.如图1,在半径为10的 中,如果弦心距
中,如果弦心距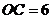 ,
,
那么弦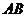 的长等于( )
的长等于( )
A.4 B.8
C.16 D.32
5.不等式组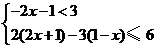 的解集为( )
的解集为( )
A.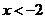 B.
B.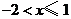 C.
C.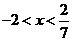 D.
D.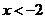 或
或
6.为建设生态滨州,我市某中学在植树节那天,组织初三年级八个班的学生到西城新区植树,各班植树情况如下表:
班级
一
二
三
四
五
六
七
八
合计
棵数
15
18
22
25
29
14
18
19
160
下列说法错误的是( )
A.这组数据的众数是18
B.这组数据的中位数是18.5
C.这组数据的平均数是20
 D.以平均数20(棵)为标准评价这次植树活动中各班植树任务完成情况比较合理
D.以平均数20(棵)为标准评价这次植树活动中各班植树任务完成情况比较合理
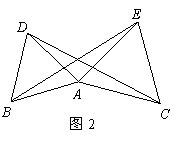
7.如图2,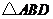 与
与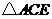 均为正三角形,且
均为正三角形,且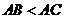 ,
,
则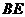 与
与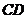 之间的大小关系是( )
之间的大小关系是( )
A.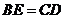 B.
B.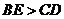
C.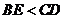 D.大小关系不确定
D.大小关系不确定
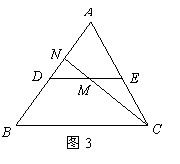 8.如图3,
8.如图3,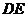 是
是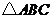 的中位线,
的中位线,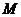 是
是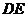 的中点,
的中点,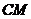 的
的
延长线交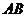 于点
于点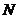 ,则
,则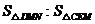 等于( )
等于( )
A.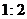 B.
B.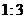
C.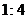 D.
D.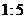
9.已知: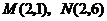 两点,反比例函数
两点,反比例函数 与线段
与线段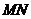 相交,过反比例函数
相交,过反比例函数 上任意一点
上任意一点 作
作 轴的垂线
轴的垂线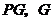 为垂足,
为垂足,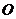 为坐标原点,则
为坐标原点,则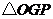 面积
面积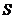 的取值范围是( )
的取值范围是( )
 A.
A.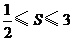 B.
B.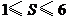 C.
C.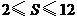 D.
D.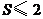 或
或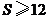
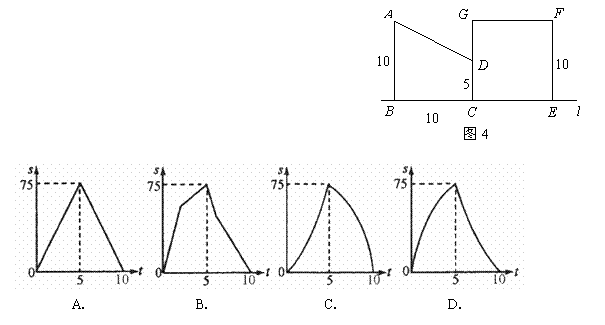
10.如图4(单位:m),直角梯形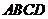 以
以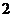 m/s的速度沿
m/s的速度沿
直线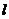 向正方形
向正方形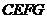 方向移动,直到
方向移动,直到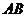 与
与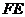 重合,直角
重合,直角
梯形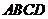 与正方形
与正方形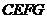 重叠部分的面积
重叠部分的面积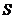 关于移动时间
关于移动时间
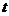 的函数图象可能是( )
的函数图象可能是( )
 第Ⅱ卷(非选择题 共30分)
第Ⅱ卷(非选择题 共30分)
二、填空题:本大题共8小题,每小题4分,共32分.把答案填在题中横线上.
11.分式方程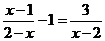 的解为
.
的解为
.
12.如图5,在距旗杆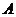 处,用测角仪测得旗杆顶端
处,用测角仪测得旗杆顶端
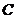 的仰角为
的仰角为 ,已知测角仪
,已知测角仪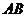 的高为
的高为
的高等于 米.
13.某同学对本地区2006年5月份连续六天的最高气温做了记录,每天最高气温与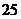 ℃的上下波动数据分别为
℃的上下波动数据分别为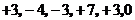 ,则这六天中气温波动数据的方差为 .
,则这六天中气温波动数据的方差为 .
 14.如图6,已知等腰梯形
14.如图6,已知等腰梯形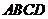 的周长是
的周长是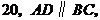
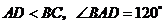 ,对角线
,对角线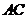 平分
平分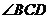 ,
,
则
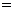 .
.
15.已知抛物线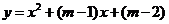 与
与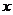 轴相交于
轴相交于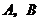 两点,且线段
两点,且线段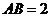 ,则
,则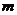 的值为
.
的值为
.
 16.已知二次函数不经过第一象限,且与
16.已知二次函数不经过第一象限,且与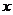 轴相交于不同的两点,请写出一个满足上述条件的二次函数解析式 .
轴相交于不同的两点,请写出一个满足上述条件的二次函数解析式 .
17.如图7,在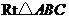 中,
中,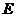 为斜边
为斜边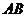 上一点,
上一点,
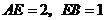 ,四边形
,四边形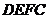 为正方形,则阴影
为正方形,则阴影
部分的面积为 .
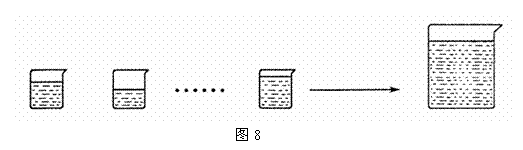
18.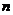 个小杯中依次盛有
个小杯中依次盛有 克糖水,并且分别含糖
克糖水,并且分别含糖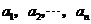 克.
克.
若这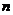 杯糖水的浓度相同,则有连等式
杯糖水的浓度相同,则有连等式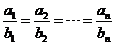 .
.
现将这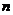 杯糖水合到一个大空杯中,则合杯糖水的浓度与各小杯糖水的浓度还是一样的.
杯糖水合到一个大空杯中,则合杯糖水的浓度与各小杯糖水的浓度还是一样的.
这个尽人皆知的事实,说明一个数学定理 等比定理:
等比定理:
若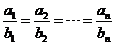 ,则
,则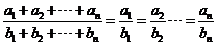 .
.
若这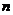 杯糖水的浓度互不相同,不妨设
杯糖水的浓度互不相同,不妨设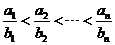 ,
,
现将这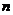 杯糖水合到一个大空杯中,则合杯糖水的浓度一定大于
,且小于 .
杯糖水合到一个大空杯中,则合杯糖水的浓度一定大于
,且小于 .
这个尽人皆知的事实,又说明了一个数学定理 不等比定理:
不等比定理:
 若
若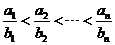 ,则
.
,则
.
三、解答题:本大题共7小题,共58分.解答应写出文字说明、证明过程或演算步骤.
19.(本小题满分5分)
解方程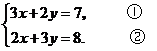
20.(本小题满分7分)
已知 ,且
,且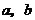 均为正数,先化简下面的代数式,再求值:
均为正数,先化简下面的代数式,再求值: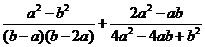 .
.
21.(本小题满分8分)
如图9,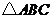 是一块锐角三角形余料,边
是一块锐角三角形余料,边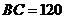 mm,高
mm,高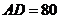 mm,要把它加工成长方形零件
mm,要把它加工成长方形零件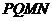 ,使长方形
,使长方形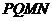 的边
的边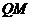 在
在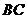 上,其余两个顶点
上,其余两个顶点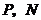 分别在
分别在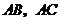 上.
上.
(Ⅰ)求这个长方形零件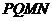 面积
面积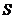 的最大值;
的最大值;
 (Ⅱ)在这个长方形零件
(Ⅱ)在这个长方形零件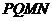 面积最大时,能否将余下的材料
面积最大时,能否将余下的材料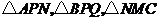 剪下再拼成(不计接缝用料及损耗)与长方形
剪下再拼成(不计接缝用料及损耗)与长方形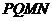 大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
22.(本小题满分8分)
假设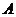 型进口汽车(以下简称
型进口汽车(以下简称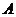 型车)关税率在2001年是100%,在2006年是25%,2001年
型车)关税率在2001年是100%,在2006年是25%,2001年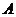 型车每辆的价格为64万元(其中含32万元的关税).
型车每辆的价格为64万元(其中含32万元的关税).
(Ⅰ)已知与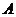 型车性能相近的
型车性能相近的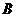 型国产汽车(以下简称
型国产汽车(以下简称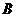 型车),2001年每辆的价格为46万元,若
型车),2001年每辆的价格为46万元,若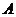 型车的价格只受关税降低的影响,为了保证2006年
型车的价格只受关税降低的影响,为了保证2006年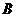 型车的价格为
型车的价格为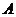 型车价格的90%,
型车价格的90%,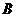 型车价格要逐年降低,求平均每年下降多少万元;
型车价格要逐年降低,求平均每年下降多少万元;
(Ⅱ)某人在2004年投资30万元,计划到2006年用这笔投资及投资回报买一辆按(Ⅰ)中所述降低价格后的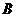 型车,假设每年的投资回报率相同,第一年的回报计入第二年的投资,试求每年的最低回报率.(参考数据:
型车,假设每年的投资回报率相同,第一年的回报计入第二年的投资,试求每年的最低回报率.(参考数据: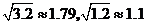 )
)
23.(本小题满分8分)
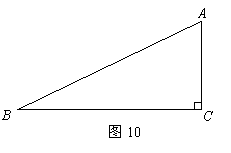
如图10,已知直角三角形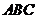 ,
,
(Ⅰ)试作出经过点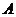 ,圆心
,圆心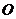 在斜边
在斜边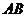 上,且与边
上,且与边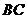 相切于点
相切于点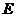 的
的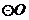 及切点
及切点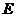 和圆心
和圆心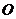 (要求:用尺规作图,保留作图痕迹,不写作法和证明);
(要求:用尺规作图,保留作图痕迹,不写作法和证明);
(Ⅱ)设(Ⅰ)中所作的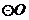 与边
与边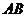 交于异于点
交于异于点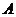 的另一点
的另一点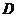 .求证:
.求证:
 (1)
(1)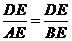 ;
;
(2)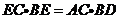 .
.
 24(本小题满分10分)
24(本小题满分10分)
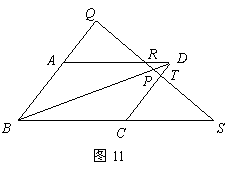
(Ⅰ)如图11,点 在
在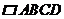 的对角线
的对角线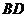 上,一直线过点
上,一直线过点 分别交
分别交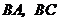 的延长线于点
的延长线于点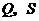 ,交
,交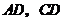 于点
于点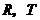 .
.
求证: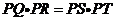 ;
;
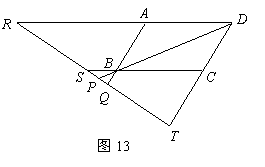
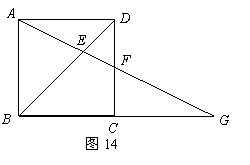
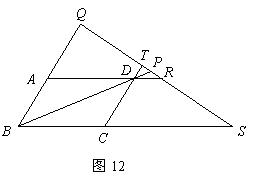 (Ⅱ)如图12,图13,当点
(Ⅱ)如图12,图13,当点 在
在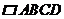 的对角线
的对角线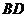 或
或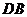 的延长线上时,
的延长线上时,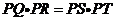 是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图12为例进行证明或说明);
是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图12为例进行证明或说明);
 (Ⅲ)如图14,
(Ⅲ)如图14,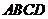 为正方形,
为正方形, 四点在同一条直线上,并且
四点在同一条直线上,并且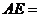
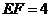 cm,试以(Ⅰ)所得结论为依据,求线段
cm,试以(Ⅰ)所得结论为依据,求线段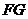 的长度.
的长度.
25.(本小题满分12分)
已知:抛物线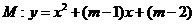 与
与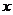 轴相交于
轴相交于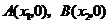 两点,且
两点,且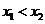 .
.
(Ⅰ)若 ,且
,且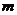 为正整数,求抛物线
为正整数,求抛物线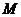 的解析式;
的解析式;
(Ⅱ)若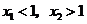 ,求
,求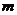 的取值范围;
的取值范围;
(Ⅲ)试判断是否存在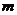 ,使经过点
,使经过点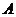 和点
和点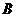 的圆与
的圆与 轴相切于点
轴相切于点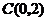 ,若存在,求出
,若存在,求出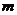 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(Ⅳ)若直线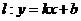 过点
过点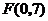 ,与(Ⅰ)中的抛物线
,与(Ⅰ)中的抛物线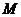 相交于
相交于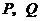 两点,且使
两点,且使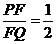 ,求直线
,求直线 的解析式.
的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com