
2007年威海市初中升学考试数学
(时间120分钟,满分120分)
亲爱的同学:
你好!答题前,请仔细阅读以下说明:
1.请将密封线内的项目填写清楚.
2.本试卷分第Ⅰ卷和第Ⅱ卷两部分,共10页.第Ⅰ卷(1至2页)为选择题,第Ⅱ卷(3至10页)为非选择题.第Ⅰ卷(选择题)的答案须填写在第3页的答案表中,第Ⅱ卷(非选择题)用兰、黑色钢笔或圆珠笔直接答在试卷上.考试结束时,将试卷全部上交.
3.凡要求保留精确度的题目,要用计算器计算;不要求保留精确度的题目,计算结果保留准确值.
希望你能愉快地度过这120分钟,祝你成功!
第Ⅰ卷(选择题,共36分)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1. 的相反数是( )
的相反数是( )
A. B.
B. C.
C. D.
D.
2.某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是( )

3.下列计算正确的是( )
A. B.
B.
 C.
C. D.
D.
4.将一副直角三角尺如图放置,已知 ,则
,则 的度数是( )
的度数是( )
A. B.
B.
C.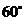 D.
D.
5.小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数
20
21
22
23
24
25
26
27
28
人数
2
4
3
8
10
9
6
3
1
A.该组数据的众数是24分 B.该组数据的平均数是25分
C.该组数据的中位数是24分 D.该组数据的极差是8分
6.已知圆锥的底面半径为6,高为8,则它的侧面积是( )
A. B.
B.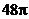 C.
C. D.
D.
7.下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
A. B.
B. C.
C. D.
D.
8.下列各式计算正确的是( )
A. B.
B.
C. D.
D.
 9.如图,直线
9.如图,直线 与双曲线
与双曲线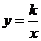 交于点
交于点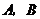 .过点
.过点 作
作 轴,垂足为点
轴,垂足为点 ,连结
,连结 .若
.若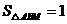 ,则
,则 的值是( )
的值是( )
A.
B.
C.
D.
10.如图,小亮在操场上玩,一段时间内沿 的路径匀速散步,能近似刻画小亮到出发点
的路径匀速散步,能近似刻画小亮到出发点 的距离
的距离 与时间
与时间 之间关系的函数图象是( )
之间关系的函数图象是( )

楼号





大桶水数/桶
38
55
50
72
85
11.如图,一条街道旁有 五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
 |
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( )
A. 楼 B.
楼 B. 楼 C.
楼 C. 楼 D.
楼 D. 楼
楼
 12.
12.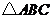 与平行四边形DEFG如图放置,点
与平行四边形DEFG如图放置,点 分别在边
分别在边 上,点
上,点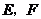 在边
在边 上.已知
上.已知 ,
, ,则
,则 的度数( )
的度数( )
A.等于 B.等于
B.等于
C.等于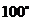 D.条件不足,无法判断
D.条件不足,无法判断
第Ⅱ卷(非选择题,共84分)
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
 13.计算:
13.计算: .
.
14.如图, 是
是 的直径,点
的直径,点 都在⊙O上,若
都在⊙O上,若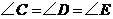 ,则
,则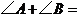 º.
º.
15.方程 的解为:
.
的解为:
.
16.将一直径为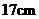 的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线折叠得到正方体(图③)形状的纸盒,则这样的纸盒体积最大为
cm3.
的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线折叠得到正方体(图③)形状的纸盒,则这样的纸盒体积最大为
cm3.
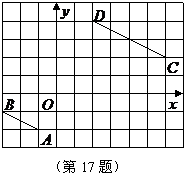 |
|||
 |
|||
17.线段 在平面直角坐标系中的位置如图所示,
在平面直角坐标系中的位置如图所示, 为坐标原点,若线段
为坐标原点,若线段 上一点
上一点 的坐标为
的坐标为 ,则直线
,则直线 与线段
与线段 的交点的坐标为
.
的交点的坐标为
.
18.观察下列等式:
 ,
, ,
, ,
, ,
, …
…
请你把发现的规律用字母表示出来: =
.
=
.
三、解答题(本大题共7小题,共66分)
19.(7分)
解不等式组,并把它的解集表示在数轴上:
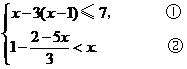
20.(7分)
甲、乙两火车站相距
21.(9分)
 如图,正方形网格的每一个小正方形的边长都是1,试求
如图,正方形网格的每一个小正方形的边长都是1,试求 的度数.
的度数.
22.(10分)
如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:
同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
(1)请你通过画树状图的方法求小颖获胜的概率.
(2)你认为该游戏规则是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.


23.(10分)
如图,一条小船从港口 出发,沿北偏东
出发,沿北偏东 方向航行
方向航行 海里后到达
海里后到达 处,然后又沿北偏西
处,然后又沿北偏西 方向航行
方向航行 海里后到达
海里后到达 处.问此时小船距港口
处.问此时小船距港口 多少海里?(结果精确到
多少海里?(结果精确到
 友情提示:以下数据可以选用:
友情提示:以下数据可以选用: ,
, ,
, ,
, .
.
24.(11分)
 如图,四边形
如图,四边形 为一梯形纸片,
为一梯形纸片, ,
,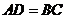 .翻折纸片
.翻折纸片 ,使点
,使点 与点
与点 重合,折痕为
重合,折痕为 .已知
.已知 .
.
(1)求证: ;
;
(2)若 ,
,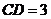 ,求线段
,求线段 的长.
的长.
25.(12分)
如图①,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,二次函数
,二次函数 的图象记为抛物线
的图象记为抛物线 .
.
(1)平移抛物线 ,使平移后的抛物线过点
,使平移后的抛物线过点 ,但不过点
,但不过点 ,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
(2)平移抛物线 ,使平移后的抛物线过
,使平移后的抛物线过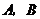 两点,记为抛物线
两点,记为抛物线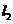 ,如图②,求抛物线
,如图②,求抛物线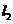 的函数表达式.
的函数表达式.
(3)设抛物线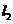 的顶点为
的顶点为 ,
, 为
为 轴上一点.若
轴上一点.若 ,求点
,求点 的坐标.
的坐标.
(4)请在图③上用尺规作图的方式探究抛物线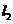 上是否存在点
上是否存在点 ,使
,使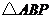 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点 共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com