
2006-2007学年度临沂市郯城县下学期期末考试
八年级数学试卷
一、选择题:下列各题所给出的四个选项中只有一项是符合题目要求的,请将其代号填入下面答题框内(每小题3分,共39分)
1.若分式 的值为零,则
的值为零,则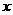 的值为
的值为
A.0 B.
2.若反比例函数 的图像在第二、四象限,则
的图像在第二、四象限,则 的值是
的值是
A.1或-l B.小于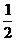 的任意实数
的任意实数
C.-l D.不能确定
3.如图,A为反比例函数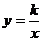 图像上一点,AB⊥
图像上一点,AB⊥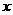 轴于点B,若
轴于点B,若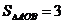 ,则
,则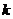 的值是
的值是
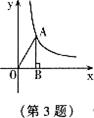
A.6 B.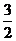 D.不能确定
D.不能确定
4.菱形、矩形、正方形都具有的性质
A.对角线相等且互相平分 B.对角线互相平分
C.对角线相等且互相垂直平分 D.四条边相等,四个角相等
5. ABC的两边长分别是3和4,若一个正方形的边长恰是
ABC的两边长分别是3和4,若一个正方形的边长恰是 ABC的第三边,则该正方形的面积是
ABC的第三边,则该正方形的面积是
A.25 B.
6.反比例函数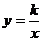 和一次函数
和一次函数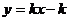 在同一直角坐标系中的图像大致是
在同一直角坐标系中的图像大致是
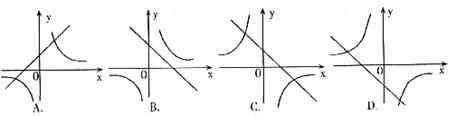
(第6题)
7.顺次连结等腰梯形四边中点所得的四边形是
A.等腰梯形 B.矩形 C.菱形 D.正方形
8.在梯形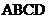 中,AD//BC,AC⊥BD,且AC=
中,AD//BC,AC⊥BD,且AC=
A.
9.已知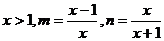 ,则
,则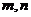 的大小关系是
的大小关系是
A.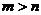 B.
B.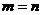 C.
C.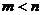 D.无法确定
D.无法确定
10.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分,若这组数据的众数与平均数恰好相等,则这组数据的中位数是
A.90分 B.85分 C.95分 D.100分
11.在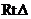 ABC中,∠C=90°,BC=6,AC=8,则斜边上的高为
ABC中,∠C=90°,BC=6,AC=8,则斜边上的高为
A. B.
B.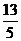 C.
C.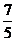 D.10
D.10
12.给出下列几组数:①6,7,8; ②8,15,16; ③9,40,41; ④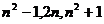 (
(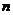 为大于1的整数)。其中能组成直角三角形的是
为大于1的整数)。其中能组成直角三角形的是
A.①③ B.②④ C.①② D.③④
13.如图,E、F分别是正方形 的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④
的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④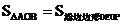 中,错误的有
中,错误的有
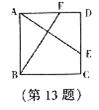
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共7小题,每小题3分,共21分)把答案直接填在题中横线上。
14.化简: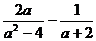 = 。
= 。
15.已知双曲线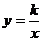 经过点(-2,6),如果A(
经过点(-2,6),如果A(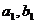 ),B(
),B(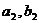 )两点在该双曲线上,且
)两点在该双曲线上,且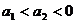 ,那么
,那么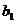
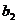 。
。
16.双曲线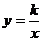 和一次函数
和一次函数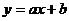 的图像的两个交点分别是A(-1,-4),B(
的图像的两个交点分别是A(-1,-4),B(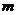 ,2),则
,2),则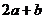 =
。
=
。
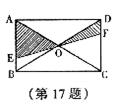
17.如图,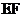 过矩形
过矩形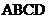 对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积与矩形
对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积与矩形 的面积的比是
的面积的比是
18.若一组数据al,a2,a3,a4,a5的方差为6,则另一组新数据3al,
19.梯形 中,
中,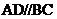 ,∠ABC=60°,BD=2
,∠ABC=60°,BD=2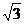 ,AE为梯形的高,且BE=1,则AD=
。
,AE为梯形的高,且BE=1,则AD=
。
20.已知四边形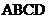 ,给出下列条件:①∠A=∠C,∠B=∠D; ②AB=BC=CD=DA;③AB//CD,AB=CD;④AC⊥BD;⑤∠A=∠C,AB//CD;⑥AB=CD,BC=AD。请你至少写出三种符合上述一个或几个条件来推出四边形
,给出下列条件:①∠A=∠C,∠B=∠D; ②AB=BC=CD=DA;③AB//CD,AB=CD;④AC⊥BD;⑤∠A=∠C,AB//CD;⑥AB=CD,BC=AD。请你至少写出三种符合上述一个或几个条件来推出四边形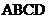 为菱形。(只填序号即可)
为菱形。(只填序号即可)
(1) ;(2) ;(3) 。
三、解答题(本大题共6个小题,共计60分)
21.(本小题满分7分)
先化简,再求值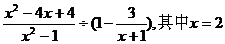 。
。
22.(本小题满分9分)
八年级(2)班学生在“五一”长假期间到外地旅游,学校距旅游区l80千米,一部分学生乘公共汽车先行,出发40分钟后,另一部分学生乘火车前往,结果他们同时到达,已知火车的速度是公共汽车的1.5倍,求两种车的速度。
23.(本小题满分8分)
如图,甲楼在乙楼的南面,它们的设计高度是若干层,每层高均为
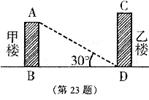
(1)若要求甲楼和乙楼的设计高度均为6层,且冬天甲楼的影子不能落在乙楼上,那么建筑时两楼之间的距离BD至少为多少米?(保留根号)
(2)由于受空间的限制,甲楼和乙楼的距离BD=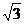 =1.732)
=1.732)
24.(本小题满分8分)
李老师为了从平时在班级里数学比较优秀的袁军、张鹏两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
袁军
74
86
84
85
87
83
84
90
89
98
张鹏
92
86
81
89
81
83
85
86
86
91
利用表中提供的数据,解答下列问题:
(1)填写完成下表:
平均成绩
中位数
众数
袁军
86
85.5
张鹏
86
86
(2)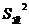 =33.2,请你帮助
=33.2,请你帮助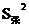 ;
;
(3)请你根据上面的信息,运用所学的统计知识,帮助
25.(本小题满分8分)
如图,在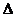 ABC中,点O是AC边上一个动点,过O点作直线MN//BC,设MN交∠
ABC中,点O是AC边上一个动点,过O点作直线MN//BC,设MN交∠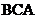 的平分线CE于点E,交∠
的平分线CE于点E,交∠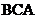 的外角平分线CF于点F。
的外角平分线CF于点F。
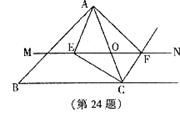
(1)求证: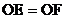 ;
;
(2)当点O运动到何处时,四边形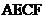 是矩形?请证明你的结论。
是矩形?请证明你的结论。
26.(本小题满分9分)
如图,平面上的四边形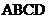 是一只“风筝”的骨架,其中AB=AD,CB=CD。
是一只“风筝”的骨架,其中AB=AD,CB=CD。
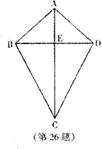
(1)八年级小明同学观察了这个“风筝”的骨架后,他认为四边形 的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意小明同学的判断吗?请充分说明理由;
的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意小明同学的判断吗?请充分说明理由;
(2)设对角线AC=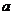 ,BD=
,BD=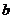 ,请用含
,请用含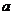 ,
,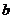 的式子表示四边形
的式子表示四边形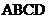 的面积。
的面积。
27.(本小题满分11分)
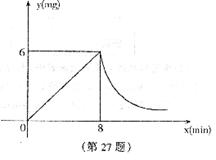
为了预防疾病.某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量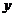 (mg)与
(mg)与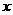 (min)成正比例,药物燃烧后,
(min)成正比例,药物燃烧后,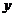 与
与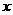 成反比例。现测得药物8min烧完,此时室内空气中每立方米的含药量为6mg,根据题中提供的信息,完成下列问题:
成反比例。现测得药物8min烧完,此时室内空气中每立方米的含药量为6mg,根据题中提供的信息,完成下列问题:
(1)药物燃烧时,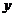 与
与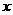 的函数关系式是
。
的函数关系式是
。
(2)药物燃烧后,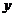 与
与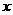 的函数关系式是
。
的函数关系式是
。
(3)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进人教室,那么从消毒开始,至少要经过 min后,学生才能回到教室。
(4)研究表明,当空气中每立方米的含药量不低于3mg,且持续时间不低于10min时,才能有效杀菌,那么此次消毒是否成功,为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com