
2006-2007学年度聊城市临清县第二学期期末考试
初二数学试卷
一、选择题:下列各题都给出了四个选项,其中只有一个选项是正确的。请把正确选项的序 号涂在答题卡上。每小题4分,共48分。
1.下列等式中,不成立的是
A.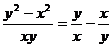 B.
B.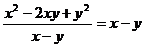
C.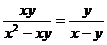 D.
D.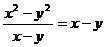
2.生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子的直径约为0.
A.0.2×10
3.如图1,点A是图象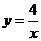 上的一点,AB⊥y轴于点B,则△AOB的面积为
上的一点,AB⊥y轴于点B,则△AOB的面积为
A.1 B.
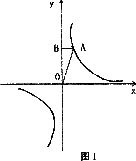
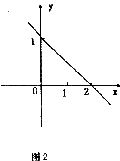
4.若函数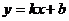 (k、b为常数)的图象如图2所示,那么,y>0时,x的取值范围是
(k、b为常数)的图象如图2所示,那么,y>0时,x的取值范围是
A.x>1 B.x<
5.正比例函数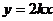 与反比例函数
与反比例函数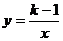 在同一直角坐标系中的图象不可能是
在同一直角坐标系中的图象不可能是

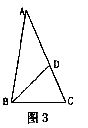
6.如图3,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于点D,则图3中共有等腰三角形
A.3个 B.2个 C.1个 D.O个
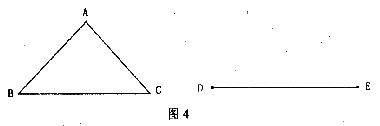
7.如图4,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形可以画出( )
A.2个 B.4个 C.6个 D.8个
8.如果kb<0,且不等式kx+b>0的解集为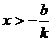 ,则函数y=kx+b的图象仅可能是
,则函数y=kx+b的图象仅可能是

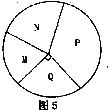
9.如图5所示,是一个正在绘制的扇形统计图,整个圆表示某班参加体育活动的总人数,那么表示参加立定跳远训练的人数占总人数的35%的扇形是
A.P B.Q C.M D.N
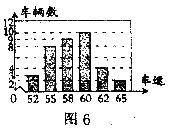 10.为了了解汽车司机遵守交通法规的意识,小明及学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速(单位:千米/小时)情况如图6所示。根据统计图分析,这组车速数据的众数和中位数分别是
10.为了了解汽车司机遵守交通法规的意识,小明及学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速(单位:千米/小时)情况如图6所示。根据统计图分析,这组车速数据的众数和中位数分别是
A.60千米/小时,60千米/小时
B.58千米/小时,60千米/小时
C.60千米/小时,58千米/小时
D.
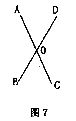
11.如图7,线段AC、BD相交于点O,欲使四边形ABCD成为等腰梯形,需要满足的条件是
A.AO=CO,BO=DO B.AO=CO,BO=DO,∠AOB=90°
C.AO=DO,BO=CO,AO≠CO D.AO=DO,∠AOB=90°
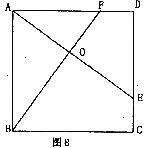
12.如图8,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△A0B=S四边形DEOF.其中错误的有
A.1个 B.2个 C.3个 D.4个
二、填空题:本题5个小题,共20分。将最后结果直接填在答题卷的相应位置。
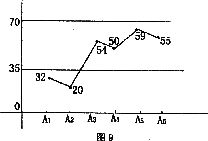
13.如图9,是一组数据的折线统计图,则这组数据的极差为 ,平均数为
14.向阳中学计划将120名学生平均分成若干个读书小组,若每个小组比原计划多1人,则比原计划少分出6个小组,那么原计划要分成多少个小组?设原计划分成x个小组,根据题意,可列方程为 。
15.已知直线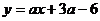 不经过第二象限,则a的取值范围是
。
不经过第二象限,则a的取值范围是
。
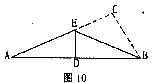
16.如图10,已知在Rt△ABC中,∠C=90°,沿过点B的一条直线BE折叠△ABC,使点C落在AB边的中点D处,则∠A的度数为 。
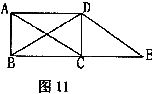
17.张老师在数学课上出了这样一道题目,如图11,延长矩形ABCD的BC到点E,使CE=BC,连接DE,试根据题中条件写出一个正确的结论。
小娜得到的结论是:△DBF是等腰三角形;
小华得到的结论是:图中与△DCE全等的三角形(不包括它本身)有4个;
小巧得到的结论是:四边形ACED是平行四边形;
小芳得到的结论是:△DCE可以看作是△DAB绕点D逆时针旋转90°得到的。你认为这四位同学所得结论正确的有 (写出全部正确学生姓名即可)。
三、解答题:本题6个小题。共52分。解答应写出必要的文字说明、证明过程或推演步骤。
18.(本题满分8分) 已知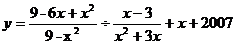 ,试说明不论
,试说明不论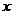 为何值时,y的值均不变。
为何值时,y的值均不变。
19.(本题满分8分)本学期期中考试时A、B、C、D、E五位同学的数学、英语成绩的有关信息,如下表所示:
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式如下:标准分=(个人成绩-平均成绩)÷成绩标准差
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考的更好?
20.(本题满分9分)随着教学手段的不断更新,要求计算器进入课堂,某电子厂家经过市场调查,发现某种计算器的供应量x(万个)与价格y1(万元)之间的函数关系如图12所示;需求量x(万个)与价格y2(万元)之间的函数关系也如图12,如果你是这个电子工厂的厂长,应计划生产这种计算器多少个,每个售价多少元,才能使市场达到供需平衡?
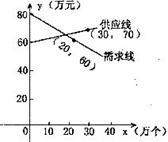
图12
21.(本题满分9分)
如图13,BF⊥AC,CE⊥AB,BE=CF。求证:AD平分∠BAC。
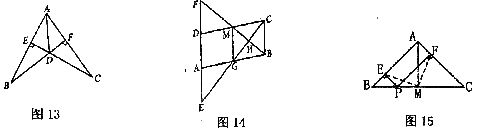
22.(本题满分9分)如图14,在平行四边形ABCD中,AB=2BC,点E在DA的延长线上,AE=AD,点F在AD的延长线上,DF=AD,CE交AB于点G,BF交CD于点M,CE与BF交于点H,
求证:四边形GBCM是菱形.
23.(本题满分9分)如图15,在△ABC中,∠BAC=90°,AB=AC,M为BC的中点,P为BC上任意一点,PE⊥AB于点E,PF⊥AC于点F,请问ME与MF相等吗?说说你的理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com