
2006-2007学年度东营市第二学期期末
质量调研初二数学试卷
一、选择题(本题共12小题,每小题4分,满分48分。下面各题给出的四个选项中,只有一项是正确的,请将正确选项的代号填在题后的答题卡内)。
1.在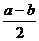 ,
,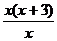 ,
, ,
,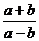 中是分式的有
中是分式的有
A.1个 B.2个 C.3个 D.4个
2.下列变形正确的是
A.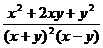 =
= B.
B.
C. D.
D.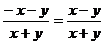
3.在△ABC中,AD是BC边上的中线,G是重心,AG=6,那么线段DG的长为
A.2 B.
4.在直角坐标系中,点P(-2,3)到原点的距离是
A. B.
B. C.
C. D.2
D.2
5.菱形、矩形、正方形都具有的性质是
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
6.反比例函数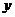 =
= 和一次函数
和一次函数 在同一直角坐标系中的图像大致是
在同一直角坐标系中的图像大致是
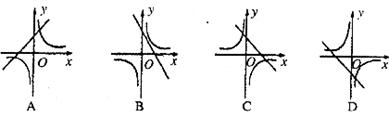
7.有两块面积相同的小麦试验田,分别收获小麦9000 kg和15000 kg,已知第一块试验田每公顷的产量比第二块少3000 kg,若设第一块试验田每公顷的产量为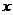 kg,根据题意,可得方程
kg,根据题意,可得方程
A.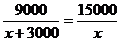 B.
B.
C.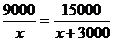 D.
D.
8.科学记数法2.02×10 ,表示的原数正确的是
,表示的原数正确的是
A.0.0000000202 B.0.000000202 C.0.00000202 D.20200000
9.为了考察月季、玫瑰两种花的苗高,分别从中抽取5株苗,测得花苗的高(单位:cm)如下:甲:2,4,6,8,10;乙:1,3,5,7,9。用S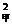 、S
、S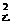 分别表示两个样本方差,那么
分别表示两个样本方差,那么
A.S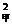 > S
> S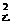 B.S
B.S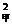 < S
< S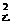
C.S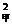 = S
= S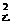 D.S
D.S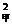 和S
和S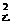 的关系不能确定
的关系不能确定
10.班主任为了了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示。那么这六位学生学习时间的众数与中位数分别是
学生姓名
小丽
小明
小颖
小华
小乐
小英
学习时间(小时)
4
6
3
4
5
8
A.4和4.5 B.4.5和4 C.4和3.5 D.3.5和4
11.如下图,已知正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为
A.9 B.10 C.11 D.12
12.如图,平面上两棵不同高度、笔直的小树,同一时刻在太阳光线照射下形成的影子分别 是AB、DC,则

A.四边形ABCD是平行四边形 B.四边形ABCD是梯形
C.线段AB与线段CD相交 D.以上三个选项均有可能
二、填空题(本大题共5小题,共20分。只要求填写最后结果,每小题填对得4分。)
13.当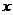 =2时,分式
=2时,分式 无意义,则当
无意义,则当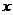 =3时,分式
=3时,分式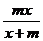 的值为
。
的值为
。
14.反比例函数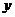 =
= 的图像在所在的每个象限内,
的图像在所在的每个象限内,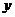 随
随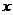 的增大而增大,则
的增大而增大,则 = 。
= 。
15.矩形的一个内角的平分线分矩形的一边为1cm和3cm两部分,则这个矩形的周长是 cm。
16.如下图,梯形纸片ABCD中,∠B=60°,AD∥BC,AB=AD=2,BC=6,将纸片折叠,使点B与点D重合,折痕为AE,则CE= 。
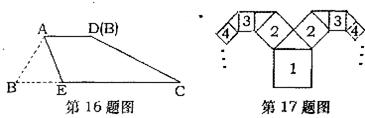
17.如上图,是一个“羊头型”的图案,其作法是:从正方形1开始以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依次类推,若正方形1的边长是64厘米,则正方形7的边长是 。
三、解答题(本大题共8小题,共82分。解答要写出必要的文字说明、证明过程或演算步骤。)
18.(本题满分8分)
解方程 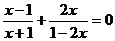
19.(本题满分8分)
已知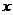 为整数,且
为整数,且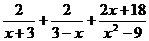 为整数,求所有符合条件的
为整数,求所有符合条件的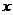 的值。
的值。
20.(本题满分10分)
如图,在平行四边形ABCD中,点E,F在BD上,且BF=DE。

(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形。
21.(本题满分l2分)
已知反比例函数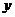 =
= 的图像经过点(4,
的图像经过点(4,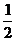 ),若一次函数
),若一次函数 的图像平移后经过该反比例函数图像上的点B(
的图像平移后经过该反比例函数图像上的点B(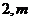 ),求平移后的一次函数图像与
),求平移后的一次函数图像与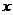 轴的交点坐标。
轴的交点坐标。
22.(本题满分8分)
学期末,某班要评选一名优秀学生干部,下表是班长、学习委员和团支部书记的得分情况:
满分
班长
学习委员
团支部书记
思想表现
30
24
28
26
学习成绩
30
26
26
24
工作能力
30
28
24
26
那么,应选谁为优秀学生干部呢?
小明说:看谁的总分高就选谁。小丽说:我不同意小明的看法,因为评选的优秀学生干部,应侧重他们的工作能力。
假设上述三个方面的重要性之比为3:3:4,那么应选谁为优秀学生干部?
23.(本题满分l0分)
王老师在一次“探究性”学习课中,设计了如下数表:

2
3
4
5
…

22?1
32?1
42?1
52?1
…

4
6
8
10
…
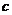
22+1
32+1
42+1
52+1
…
(1)请你分别观察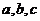 与
与 之间的关系,并用含自然数,
之间的关系,并用含自然数, 的代数式表示
的代数式表示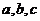 。
。
(2)猜想:以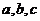 为边的三角形是否为直角三角形?并证明你的猜想。
为边的三角形是否为直角三角形?并证明你的猜想。
24.(本题满分l2分)
如图,四边形ABCD是直角梯形,∠B=90°,AB=8 cm,AD=24 cm,BC=26cm,点P从A出发,以l cm/s的速度向D运动,点Q从C同时出发,以3 cm/s的速度向B运动。其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,经过多少时间,四边形PQCD成为平行四边形?成为等腰梯形?

25.(本小题满分l4分)
我市黄河人海口是全国著名的生态自然保护区。下表与下图是该景点一周的抽样统计观光人数和门票价格。
星期
一
二
三
四
五
六
日
人数
100
120
100
100
160
230
240
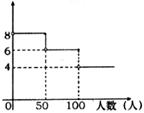
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数、众数和平均数,分析表中数据还可得到一些信息,如双休日参观人数远远高于平时等,请尝试再写出两条相关信息;
(2)若“五一”黄金周有甲、乙两个旅游团到该景点参观,两团人数之和恰为上述样本数据的中位数,乙团人数不超过50人,设两团分别购票共付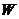 元,甲团人数为
元,甲团人数为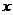 人。①求
人。①求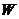 关于
关于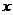 的函数关系式,并写出自变量的取值范围;②若甲团人数不超过l00人,请说明两团合起来购票比分开购票最多可节约多少钱?
的函数关系式,并写出自变量的取值范围;②若甲团人数不超过l00人,请说明两团合起来购票比分开购票最多可节约多少钱?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com