
2007年临沂市郯城中考模拟试题(三)
数学试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。满分l20分,考试时间l20分钟。
第I卷 (选择题 共39分)
一、选择题(本题共13小题,每小题3分,共39分)在每小题所给的四个选项中,只有一项是符合题目要求的)。
1.2的倒数是( )
A.-2 B.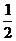 C.
C.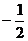 D.1
D.1
2.反比例函数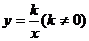 的图像经过点(1,-3),则k的值为( )
的图像经过点(1,-3),则k的值为( )
A.-3 B.3 C.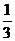 D.
D.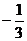
3.今年1―3月份,我市累计完成地方一般预算收入116.28亿元,数据116.28亿精确到( )
A.百亿位 B.亿位 C.百万位 D.百分位
4.下列各式从左到右的变形正确的是( )
A. B.
B.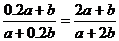
C.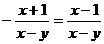 D.
D.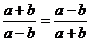
5.在Rt△ABC中,∠C=90°,AB=5,AC=3,则sinB的值是( )
A.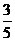 B.
B.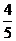 C.
C.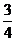 D.
D.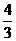
6.已知两圆的半径分别为1和4,圆心距为3,则两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
7.张华同学的身高为
A.
8.要调查某校初三学生周日的睡眠时间,选取调查对象最合适的是( )
A.选取一个班级的学生 B.选取50名男生
C.选取50名女生 D.随机选取50名初三学生
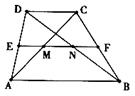
9.如图,在梯形ABCD中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=
A.
10.如图,矩形ABCD的边AB= (秒)之间的函数关系的图像是( )
(秒)之间的函数关系的图像是( )

11.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AC与BC交于点F(如下图),则CF的长为( )

A.0.5 B.0.75 C.1 D.1.25
12.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则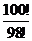 的值为( )
的值为( )
A.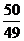 B.99! C.9900 D.2!
B.99! C.9900 D.2!
13.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽。如图,圆锥帽底半径为

A.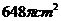 B.
B.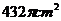 C.
C.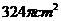 D.
D.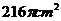
第Ⅱ卷(非选择题 共81分)
二、填空题(本大题共3小题,每小题7分,共21分)
14.国务院总理温家宝
15.如图,在△ABC中,∠C=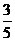 ,则BC的长是____________。
,则BC的长是____________。
16.如图,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的两端在CD、AD上滑动,当DM=___________时,△ABE与以D、M、N为项点的三角形相似。
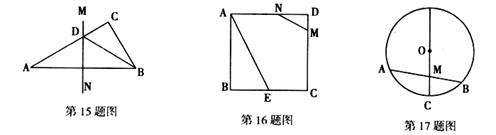
17.如图,⊙O的直径CD与弦AB(非直径)交于点M,添加一个条件:___________,就可得到点M是AB的中点.
18.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形___________。(请填图形下面的代号)

19.如图,是由若干盆花组成的形如正多边形的图案,每条边(包括两个顶点)有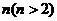 盆花,每个图案中花盆总数为S,按此规律推断S与
盆花,每个图案中花盆总数为S,按此规律推断S与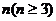 的关系式是:S=__________。
的关系式是:S=__________。
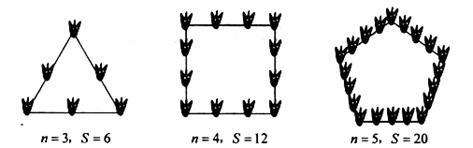
 20.如图,点M是直线
20.如图,点M是直线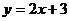 上的动点,过点M作MN垂直于
上的动点,过点M作MN垂直于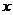 轴于点N,
轴于点N, 轴上是否存在点P使△MNP为等腰直角三角形。小明发现:当动点M运动到(-1,1)时,
轴上是否存在点P使△MNP为等腰直角三角形。小明发现:当动点M运动到(-1,1)时, 轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形。那么,在
轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形。那么,在 轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标________。
轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标________。
三、解答题:(本大题8个小题,共60分)
21.(4分)
计算: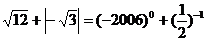
22.(6分)
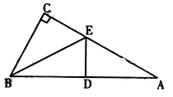
如图,在Rt△ABC中,∠C=90°,沿过点B的直线BE折叠这个三角形,要使点C恰好与AB的中点D重合,还应添加什么条件?
23.(本题满分8分)
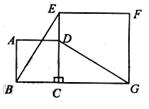
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG。
(1)观察猜想BE与DG之间的大小关系,并证明你的结论。
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,请说明理由。
24.(6分)
某商厦张贴巨幅广告:“真情回报顾客”活动共设奖金20万元,最高奖每份1万元,平均每份奖金200元,一顾客幸运地抽到一张奖券,奖金数为10元,她调查了周围正兑奖的其他顾客,一个也没有超过50元的,她气愤地要求与商厦领导评理。商厦领导说不存在欺骗,并向她出示了下面这张奖金分配表,你认为商厦说“平均每份奖金200元”是否欺骗了顾客?大多数中奖者获得的奖金能接近奖金的平均数吗?中一等奖的概率是多少?以后遇到开奖的问题你应该更关心什么?
奖金等级
一等奖
二等奖
三等奖
四等奖
五等奖
奖金额(元)
10000
6000
1000
50
10
中奖人数
3
10
87
350
550
小东同学的做法是:设新正方形的边长为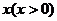 。依题意,割补前后图形的面积相等,有
。依题意,割补前后图形的面积相等,有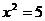 ,解得
,解得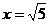 。由此可知新正方形的边长等于两个正方形组成的矩形对角线的长。于是,画出如图2所示的分割线,拼出如图3所示的新正方形。
。由此可知新正方形的边长等于两个正方形组成的矩形对角线的长。于是,画出如图2所示的分割线,拼出如图3所示的新正方形。
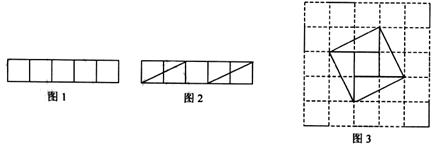
请你参考小东同学的做法,解决如下问题:
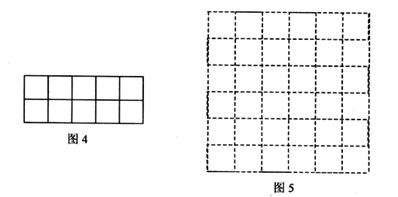
现有l0个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形。要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。说明:直接画出图形,不要求写分析过程。
解:
26.(本题满分l0分)
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半。类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角。
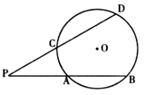
(1)判断:图中有没有圆外角?如果有,请用字母表示出来。
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系?将你的发现,用文字表述出来,并说明理由。
27.(本题满分l0分)
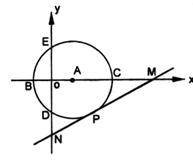
如图,在直角坐标系中,以点A(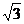 ,0)为圆心,以
,0)为圆心,以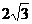 为半径的圆与
为半径的圆与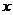 轴交于B、C两点,与
轴交于B、C两点,与 轴交于D、E两点。
轴交于D、E两点。
(1)求D点坐标。
(2)若B、C、D三点在抛物线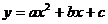 上,求这个抛物线的解析式。
上,求这个抛物线的解析式。
(3)若⊙A的切线交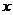 轴正半轴于点M,交
轴正半轴于点M,交 轴负半轴于点N,切点为P,
轴负半轴于点N,切点为P,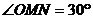 ,试判断直线MN是否经过所求抛物线的顶点?说明理由。
,试判断直线MN是否经过所求抛物线的顶点?说明理由。
28.(本题满分l2分)
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,∠C=60°,AD=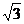 cm/s的速度向点A运动,⊙O1的半径为
cm/s的速度向点A运动,⊙O1的半径为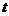 s。
s。
(1)请求出⊙O2与腰CD相切时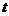 的值;
的值;
(2)在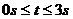 范围内,当
范围内,当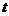 为何值时,⊙O1与⊙O2外切?
为何值时,⊙O1与⊙O2外切?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com