
2007年临沂市郯城县中考模拟试题(四)
数学试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。满分l20分。考试时间l20分钟。
第I卷(选择题 共39分)
一、选择题(本题共13小题,每小题3分,共39分)在每小题所给的四个选项中,只有一项是符合题目要求的)
1.-5的相反数是( )
A.5 B.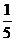 D.
D.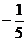
2.下列各式运算正确的是( )
A.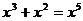 B.
B.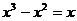
C.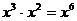 D.
D.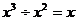
3.不等式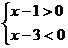 的解集是( )
的解集是( )
A.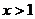 B.
B.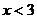 C.
C.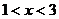 D.无解
D.无解
4.已知一次函数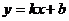 (
(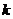 、
、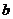 是常数,且
是常数,且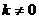 ),
),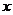 与
与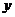 的部分对应值如下表所示,那么不等式
的部分对应值如下表所示,那么不等式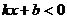 的解集是( )
的解集是( )
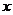
-2
-1
0
1
2
3
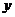
3
2
1
0
-1
-2
A.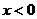 B.
B.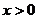 C.
C.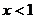 D.
D.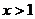
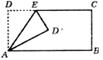 5.将矩形ABCD沿AE折叠,得到如下图所示的图形,已知
5.将矩形ABCD沿AE折叠,得到如下图所示的图形,已知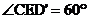 ,则∠AED的大小是( )
,则∠AED的大小是( )
A.60º B.50º
C.75º D.55º
6.亮亮准备用自己节省的零花钱买一台英语复读机,他现在已存有45元,计划从现在起以后每个月节省30元,直到他至少有300元。设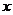 个月后他至少有300元,则可以用于计算所需要的月数的不等式是( )
个月后他至少有300元,则可以用于计算所需要的月数的不等式是( )
A.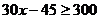 B.
B.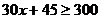
C.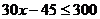 D.
D.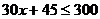
7.如果用□表示1个立方体,用 表示两个立方体重叠,用■表示三个立方体重叠,那么,如图l,是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体重叠,用■表示三个立方体重叠,那么,如图l,是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )

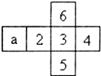 8.如右图是一个正方体纸盒的展开图,每个面内都标注了字母或数字,则面a在展开前所对的面的数字是( )
8.如右图是一个正方体纸盒的展开图,每个面内都标注了字母或数字,则面a在展开前所对的面的数字是( )
A.2 B.3
C.4 D.5
9.计算: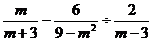 的结果为( )
的结果为( )
A.1 8.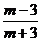 C.
C.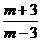 D.
D.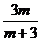
10.已知二次函数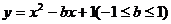 ,当
,当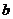 从-l逐渐变化到1的过程中,它所对应的抛物线位置也随之变动。下列关于抛物线的移动方向的描述中,正确的是( )
从-l逐渐变化到1的过程中,它所对应的抛物线位置也随之变动。下列关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动;
B.先往左下方移动,再往左上方移动;
C.先往右上方移动,再往右下方移动;
D.先往右下方移动,再往右上方移动
11.已知⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么以P为圆心,且与⊙O相切的圆的半径一定是( )
A.1或5 B.1 C.5 D.1或7
12.如下图,图l表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域,小明想同时看到该建筑物的三个侧面,他应在( )
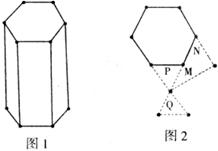
A.P区域 B.Q区域 C.M区域 D.N区域
13.水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示。某天0点到6点,该水池的蓄水量与时间的关系如图丙所示。
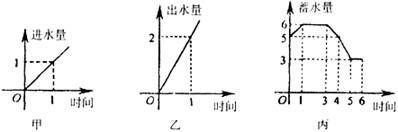
下列论断:①O点到l点,打开两个进水口,关闭出水口;②1点到3点,同时关闭两个进水口和一个出水口;③3点到4点,关闭两个进水口,打开出水口;④5点到6点,同时打开两个进水口和一个出水口。其中,可能正确的论断是( )
A.①③ B.①④ C.②③ D.②④
第Ⅱ卷(非选择题 共81分)
二、填空题(共7小题,每小题3分,计21分)
14.请你写出一个比0.1小的有理数 。
15.分解因式: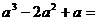 。
。
16.分式方程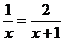 的解是
的解是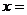 。
。
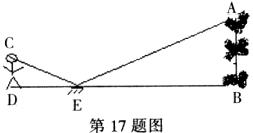
17.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为 米(精确到0.1米)。

18.一青蛙在如图8×8的正方形(每个小正方形的边长为l)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为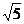 ,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是
。
,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是
。

19.某种蓄电池的电压为定值,使用此电源时,电流I(A)与可变电阻R(Ω)之间的函数关系如图所示,当用电器的电流为l0A时,用电器的可变电阻为 Ω。
20.用两块大小相同的等腰直角三角形纸片做拼图游戏,则下列图形:
①平行四边形(不包括矩形、菱形、正方形);②矩形(不包括正方形);③正方形;④等边三角形;⑤等腰直角三角形,其中一定能拼成的图形是 。(只填序号)
三、解答题(本题共8小题,共60分)
21.(本题满分6分)
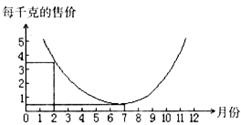
某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如下图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系。
观察图像,你能得到关于这种蔬菜销售情况的哪些信息?
答题要求:
(1)请提供四条信息; (2)不必求函数的解析式。
22.(本题满分6分)
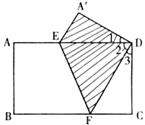
把一个矩形纸片如图折叠,使顶点B和D重合,折痕为EF。
问题:(1)找出图中全等的三角形,并证明。
(2)重合部分是什么图形?证明你的结论。
(3)连结BE,判断四边形BEDF是什么特殊四边形,BD与EF有什么关系?并证明。
23.(本题满分6分)
某校科技夏令营的学生在3位老师的带领下,准备赴北京大学参观,体验大学生活。现有两家旅行社前来洽谈,报价均为每人2000元,且各有优惠。希望旅行社表示:带队老师免费,学生按8折收费;青春旅行社表示师生一律按7折收费。经核算发现,参加两家旅行社的实际费用正好相等。
(1)该校参加科技夏令营的学生共有多少人?
(2)如果又增加了部分学生,学校应选择哪家旅行社?为什么?
24.(本题满分6分)
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工
管理人员
普通工作人员
人员结构
总经理
部门经理
科研人员
销售人员
高级技工
中级技工
勤杂工
员工数(名)
1
3
2
3
24
l
每人月工资(元)
21000
8400
2025
2200
1800
1600
950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数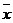 为2500元,中位数为 元,众数为 元;
为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员。请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;

(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资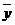 (结果保留整数),并判断
(结果保留整数),并判断 能否反映该公司员工的月工资实际水平。
能否反映该公司员工的月工资实际水平。
25.(本题满分8分)
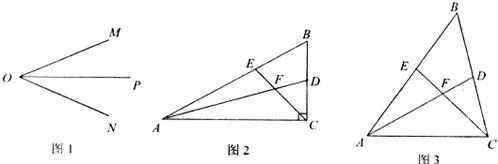
如图l,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60º,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F。请你判断并写出FE与FD之间的数量关系;
(2)如图3,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
26.(本题满分8分)
如图,已知O为原点,点A的坐标为(4, 3),OA的半径为2。过A作直线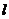 平行于
平行于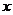 轴,点P在直线
轴,点P在直线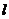 上运动。
上运动。
(1)当点P在⊙A上时,请你直接写出它的坐标;
(2)设点P的横坐标为12,试判断直线OP与⊙A的位置关系,并说明理由。
27.(本题满分l0分)
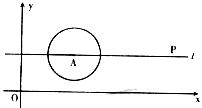
 某通讯器材公司销售一种市场需求较大的新型通讯主产品,已知每件产品的进价为40元,每年所销售该种产品的总开支(不含进价)总计120万元。在销售过程中发现,年销售量(万件)与销售单价(元)之间存在着如右图所示的一次函数关系。
某通讯器材公司销售一种市场需求较大的新型通讯主产品,已知每件产品的进价为40元,每年所销售该种产品的总开支(不含进价)总计120万元。在销售过程中发现,年销售量(万件)与销售单价(元)之间存在着如右图所示的一次函数关系。
(1)求与的函数关系式。
(2)试写出该公司销售该种产品的年获利(万元)关于销售单价(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支)。当销售单价为何值时,年获利最大?并求这个最大值。
(3)若公司希望该项种产品一年销售的获利不低于40万元,借助(2)中函数图像,请你帮助该公司确定销售单价的范围,在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
28.(本题满分l0分)
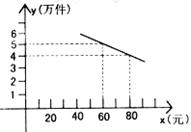
 如右图,一次函数
如右图,一次函数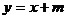 图像过点A(1, 0),交
图像过点A(1, 0),交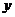 轴于点B,C为
轴于点B,C为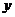 轴负半轴上一点,且BC=2OB,过A、C两点的抛物线交直线AB于点D,且CD∥
轴负半轴上一点,且BC=2OB,过A、C两点的抛物线交直线AB于点D,且CD∥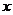 轴。
轴。
(1)求这条抛物线的解析式;
(2)观察图像,写出使一次函数值小于二次函数值时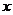 的取值范围;
的取值范围;
(3)在题中的抛物线上是否存在一点M,使得∠ADM为直角?若存在,求出点M的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com