
2007年数学江西九江中考预测试卷(二)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷120分,时间:120分钟
第Ⅰ卷(选择题共30分)
一、选择题 (共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的)
1.冬季的一天室内温度是
A.
2.如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )

A.4 B.
3.化简 +
+ 的结果是( )
的结果是( )
A. B.
B. C.
C. D.
D.
4.如果从一卷粗细均匀的电线上截取
A.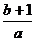 米 B.
米 B. 米 C.
米 C. 米 D.
米 D. 米
米
5.如图,⊙O是△ABC的外接圆,连接OA、OC,⊙O的半径R=2,sinB= ,则弦AC的长为( )
,则弦AC的长为( )

A.3 B. C.
C.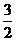 D.
D.
6.小颖的家与学校的距离为s0千米,她从家到学校先以匀速v1跑步前进,后以匀速v2(v2<v1)走完余下的路程,共用了t0小时,下列能大致表示小颖离家的距离y(千米)与离家时间t(小时)之间关系的图象是( )

A B C D
7.如图农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( ).
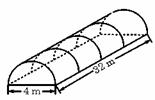
A.64π m2 B.72π m
8.已知抛物线y=2x2-4x-1,下列说法中正确的是( )
A.当x=1时,函数取得最小值y=3 B.当x=-1时,函数取得最小值y=3
C.当x=1时,函数取得最小值y=-3 D.当x=-1时,函数取得最小值y=-3
9.为了美化校园,同学们要在一块正方形空地上种上草,他们设计了图4所示的图案,其中阴影部分为绿化面积,哪个图案的绿化面积与其他图案的绿化面积不相等( ).

10.如图,在□ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有( ).

A.7 B.
第Ⅱ卷(非选择题 共90分)
二、填空题 (共6小题,每小题3分,计18分)
11.如果关于x的不等式(a-1)x<a+5和2x<4的解集相同,则a的值为 .
12.用计算器比较大小:
 (填“>”、“=”、“<”).
(填“>”、“=”、“<”).
13.杏花村现有手机188部,比2004年底的3倍还多17部,则该村2004年底有手机 部.
14.若矩形的面积为6,则矩形的长y关于宽x(x>0)的函数关系式为 .
15.小明的身高是
16.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为 .

三、解答题(共9小题,计72分,解答应写出过程)
17.(5分)用换元法解分式方程:
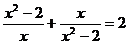
18.(本题满分6分)
如图,作△ABC的中线AD,并将△ADC绕点D旋转180°,那么点C与点B重合,点A转到A′点,不难发现AC=A′B,AD=A′D,BD=DC,如果知道AB=4 cm,AC=3 cm,你能求出中线AD的范围吗?

19.(8分)
甲乙两人掷一对骰子,若甲掷出的点数之和为6,则加一分,否则不得分;乙掷出的点数之和为7,则加一分,否则不得分;甲、乙各掷骰子10次,得分高者胜.
(1)请用列表法求出甲获胜的概率;
(2)这个游戏公平吗?若公平,说明理由;如果不公平,请你修改规则,使之公平.
20.(8分)
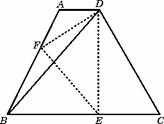
如图等腰梯形ABCD中,AD//BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E.若AD=2,BC=8.
求(1)BE的长;(2)∠CDE的正切值.
21.(8分)如图,l1、l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(小时)的函数图象,假设两种灯的使用寿命都是
2 000小时,照明效果一样.
(1)根据图象分别求出l1、l2的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

22.(9分)某研究性学习小组,为了了解本校初一学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分钟),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:
(1)这个研究性学习小组所抽取样本容量是多少?
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过.120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?

23.(9分)已知某山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(单位:米)
0
100
200
300
400
500
……
平均气温(单位:℃)
22
21.5
21
20.5
20
19.5
……
(1)若海拔高度用x(米)表示,平均气温用y(℃)表示,试写出y与x之间的函数关系式;
(2)若某种植物适宜生长在
24.(10分)已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线PA上截取PD=PC,连接CD,并延长交⊙O于点E.
(1)求证:∠ABE=∠BCE;
(2)当点P在AB的延长线上运动时,判断sin∠BCE的值是否随点P位置的变化而变化,提出你的猜想并加以证明.

25.(9分)在△CDE中,∠C=90°,CD,CE的长分别为m,n,且DE?cosD=cotE.
(1)求证m2=n;
(2)若m=2,抛物线y=a(x―m)2+n与直线y=3x+4交于A(x1,y1)和B(x2,y2)两点,且△AOB的面积为6(O为坐标原点),求a的值;
(3)若是k2= ,c+l-b=0,抛物线y=k(x2+bx+c)与x轴只有一个交点在原点的右侧,试判断抛物线与y轴的交点在y轴的正半轴还是负半轴,并证明你的结论.
,c+l-b=0,抛物线y=k(x2+bx+c)与x轴只有一个交点在原点的右侧,试判断抛物线与y轴的交点在y轴的正半轴还是负半轴,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com