
2007年贵阳市初中毕业生学业考试试卷
数学
考生注意:
1.本卷共8页,三大题共25小题.满分为150分,考试时间为120分钟,考试形式为闭卷.
2.考试时可以使用科学计算器.
一、选择题(以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,请把正确选项的字母选入该题的括号内,每小题4分,共20分)
1.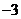 的倒数是( )
的倒数是( )
A.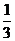 B.
B. C.
C. D.
D.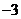
2.据2006年末的统计数据显示,免除农村义务教育阶段学杂费的西部地区和部分中部地区的学生约有52000000名,这个学生人数用科学记数法表示正确的是( )
A. B.
B. C.
C.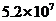 D.
D.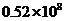
3.小明五次跳远的成绩(单位:米)是:3.6,3.8,4.2,4.0,3.9,这组数据的中位数是( )
A.
4.如左图所示,将长为
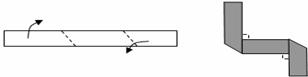
A. B.
B. C.
C. D.
D.
5.平面直角坐标系中有六个点 ,
, ,
, ,
,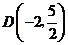 ,
,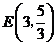 ,
,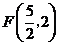 ,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是
,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是
A.点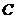 B.点
B.点 C.点
C.点 D.点
D.点
二、填空题(每小题3分,共30分)
6.比较大小:
 (填“
(填“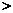 ,
, 或
或 ”符号)
”符号)
7.分解因式: .
.
8.方程 的解为
的解为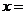 .
.
9.如图, 是圆O上三点,
是圆O上三点, ,则
,则 等于 度.
等于 度.

10.在一次抽奖活动中,中奖概率是0.12,则不中奖的概率是 .
11.在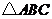 中,若
中,若 ,
,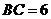 ,则第三边
,则第三边 的长度
的长度 的取值范围是
.
的取值范围是
.
12.如图,小亮从 点出发前进
点出发前进 ,向右转
,向右转 ,再前进
,再前进 ,又向右转
,又向右转 ,…,这样一直走下去,他第一次回到出发点
,…,这样一直走下去,他第一次回到出发点 时,一共走了
m.
时,一共走了
m.

13.如图,是甲、乙两地5月下旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为: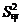
 .
.

14.如图,正方形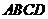 的边长为
的边长为 ,
,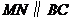 分别交
分别交 于点
于点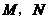 ,在
,在 上任取两点
上任取两点 ,那么图中阴影部分的面积是
.
,那么图中阴影部分的面积是
.

15.如图,某机械传动装置在静止状态时,连杆 与点
与点 运动所形成的
运动所形成的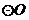 交于
交于 点,现测得
点,现测得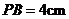 ,
,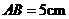 .圆O的半径
.圆O的半径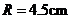 ,此时
,此时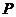 点到圆心
点到圆心 的距离是
的距离是
cm.

三、解答题
16.(本题满分7分)
如图,方格中有一条美丽可爱的小金鱼.
(1)若方格的边长为1,则小鱼的面积为 .(3分)
(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程).(4分)

(2)求表(1)中 的值.(4分)
的值.(4分)
(3)该校学生平均每人读多少本课外书?(2分)


18.(本题满分10分)
二次函数 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程 的两个根.(2分)
的两个根.(2分)
(2)写出不等式 的解集.(2分)
的解集.(2分)
(3)写出 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围.(2分)
的取值范围.(2分)
(4)若方程 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.(4分)
的取值范围.(4分)

19.(本题满分10分)
如图,一枚运载火箭从地面 处发射,当火箭到达
处发射,当火箭到达 点时,从地面
点时,从地面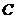 处的雷达站测得
处的雷达站测得 的距离是
的距离是 ,仰角是
,仰角是 .
. 后,火箭到达
后,火箭到达 点,此时测得
点,此时测得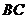 的距离是
的距离是 ,仰角为
,仰角为 ,解答下列问题:
,解答下列问题:
(1)火箭到达 点时距离发射点有多远(精确到0.01km)?(4分)
点时距离发射点有多远(精确到0.01km)?(4分)
(2)火箭从 点到
点到 点的平均速度是多少(精确到0.1km/s)?(6分)
点的平均速度是多少(精确到0.1km/s)?(6分)

20.(本题满分12分)
如图,在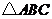 中,
中, 是
是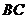 边上的一点,
边上的一点, 是
是 的中点,过
的中点,过 点作
点作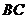 的平行线交
的平行线交 的延长线于
的延长线于 ,且
,且 ,连结
,连结 .
.
(1)求证: 是
是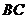 的中点.(6分)
的中点.(6分)
(2)如果 ,试判断四边形
,试判断四边形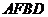 的形状,并证明你的结论.(6分)
的形状,并证明你的结论.(6分)

21.(本题满分9分)
如图,平面内有公共端点的六条射线 ,
, ,
, ,
, ,
, ,
, ,从射线
,从射线 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上.(3分)
(2)请任意写出三条射线上数字的排列规律.(3分)
(3)“2007”在哪条射线上?(3分)

22.(本题满分10分)
甲、乙两人骑自行车前往 地,他们距
地,他们距 地的路程
地的路程 与行驶时间
与行驶时间 之间的关系如图所示,请根据图象所提供的信息解答下列问题:
之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两人的速度各是多少?(4分)
(2)写出甲、乙两人距 地的路程
地的路程 与行驶时间
与行驶时间 之间的函数关系式(任写一个).(3分)
之间的函数关系式(任写一个).(3分)
(3)在什么时间段内乙比甲离 地更近?(3分)
地更近?(3分)

23.(本题满分10分)
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量 (箱)与销售价
(箱)与销售价 (元/箱)之间的函数关系式.(3分)
(元/箱)之间的函数关系式.(3分)
(2)求该批发商平均每天的销售利润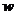 (元)与销售价
(元)与销售价 (元/箱)之间的函数关系式.(3分)
(元/箱)之间的函数关系式.(3分)
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?(4分)
24.(本题满分12分)
小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率.(4分)
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?(4分)
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.(4分)
25.(本题满分12分)
如图,从一个直径是2的圆形铁皮中剪下一个圆心角为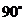 的扇形.
的扇形.
(1)求这个扇形的面积(结果保留 ).(3分)
).(3分)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.(4分)
(3)当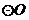 的半径
的半径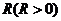 为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)
为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com