
2007-2008学年度潍坊市昌邑第一学期期末考试
九年级数学试题
一、选择题(每小题3分,共30分)
1.方程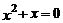 的解是( )
的解是( )
A.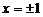 B.
B.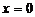 C.
C.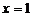 D.
D.
2.从一块正方形的木板上锯掉
A.
3.如图,已知△ACD∽△ADB,AC=4,AD=2则AB的长为( )

A.1 B. C.2 D.
C.2 D.
4.在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的值是( )
,则边AC的值是( )
A. B.
B. D.
D.
5.在Rt△ABC中,∠C=90°,下列式子中不一定成立的是( )
A.sinA=cosB
B.sinB=cosA C.tanA=tanB
D.sin
6.某学校准备改善原有楼梯的安全性能,把倾角由45°减至30°,已知原楼梯长为
A. B.
B. C.
C.
7.关于抛物线 的说法,正确的是( )
的说法,正确的是( )
A.开口向上
B.对称轴是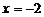 C.最大值是1 D.顶点坐标是(2,5)
C.最大值是1 D.顶点坐标是(2,5)
8.已知二次函数 的图象如图所示,下列结论:
的图象如图所示,下列结论:
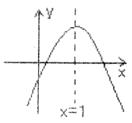
(1)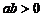 (2)
(2)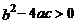 (3)
(3)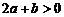 (4)
(4)
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.某校为了了解本校初三学生的体重情况,从中抽取60名学生进行测量,下列说法:
(1)总体是指本校全体初三学生 (2)个体是指每一名学生
(3)样本容量是指60名学生 (4)样本是指这60名学生的体重
正确的有( )
A.1个 B.2个 C.3个 D.4个
10.下列调查合适的是( )
A.为了解全国中学生每天学习的时间,应采取普查的方式
B.为了解2007年春节晚会的收视情况,应采取普查的方式
C.为了确保“神州”六号的成功发射,对各零件需要检查,应采取抽样调查的方式
D.为了解某森林的树种分布情况,应采用抽样调查的方式
二、填空题(每小题3分,共30分)
1.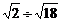 =_______________.
=_______________.
2.关于 的方程
的方程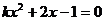 有两个不相等的实数根,则
有两个不相等的实数根,则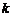 的取值范围是__________.
的取值范围是__________.
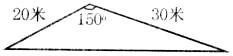
3.某市计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价 元,则购买这种草皮至少需要______________元。
元,则购买这种草皮至少需要______________元。
4.已知抛物线 的顶点坐标是(-1,4),则
的顶点坐标是(-1,4),则 =_______,
=_______, =________.
=________.
5.某人从地面沿着坡度 的山坡走了
的山坡走了
6.△ABC中,若 ,则∠C=__________.
,则∠C=__________.
7.将二次函数 的图象向________平移3个单位,再向________平移5个单位得到二次函数
的图象向________平移3个单位,再向________平移5个单位得到二次函数 的图象.
的图象.
8.抛物线 过点A(1,0),B(5,0)则此抛物线的对称轴是直线
过点A(1,0),B(5,0)则此抛物线的对称轴是直线 =_______.
=_______.
9.冰柜里装有四种饮料:5瓶特种可乐、12瓶普通可乐、9瓶橘子水、6瓶啤酒,其中特种可乐和普通可乐是含有咖啡因的饮料,那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率是_________.
10.一个口袋中装有黑球10个和白球若干个,从口袋中随机摸出一球记下颜色,再把它放回袋中摇匀,重复上述实验共100次,其中有75次摸到白球.那么估计袋中约有白球______________个.
三、解答题(60分)
1.解方程: (本小题4分)
(本小题4分)
2.求下列各式的值(每小题4分,共8分)
(1)
(2)
3.数 、
、 在数轴上的位置如图所示,
在数轴上的位置如图所示,

化简: (本小题4分)
(本小题4分)
4.如图,在△ABC中,AB=10,AC=16,BC=14,一直线分别交AB,AC于点E、F,AE=6,且△AEF与原三角形相似,求EF的长.(本小题6分)

5.已知二次函数 的图象与
的图象与 轴交于点(0,-6).与
轴交于点(0,-6).与 轴的一个交点为(-3,0).
轴的一个交点为(-3,0).
(1)求这个二次函数的解析式.
(2)求它与 轴的另一个交点的坐标.(本小题6分)
轴的另一个交点的坐标.(本小题6分)
6.在一个布口袋中装着只有颜色不同,其他都相同的白、红、黑三种颜色的小球各1只,甲乙两人进行摸球游戏:甲先从袋中摸出一球看清颜色后放回,再由乙从袋中摸出一球.
(1)试用树状图(或列表法)表示摸球游戏所有可能的结果;
(2)如果规定:乙摸到与甲相同颜色的球为乙胜,否则为负,试求乙在游戏中能获胜的概率。(本小题满分6分)
7.某农户种植花生,原来种植的花生亩产量为 ,求新品种花生亩产量的增长率.
,求新品种花生亩产量的增长率.
(本小题8分)
8.一艘轮船自西向东航行,如图所示,在A处测得东偏北21.3°(即∠A=21.3°)方向有一座小岛C,继续向东航行
(参考数据 ) (8分)
) (8分)

9.某公司推出一种新型环保产品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)表示了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系),根据图象提供的信息,解答下面的问题:
(1)由已知图象上的三点坐标,求累积利润S(万元)与销售时间t(月)之间的函数关系式;
(2)截止到几月末公司累积利润可达到30万元?
(3)第8个月公司所获利润是多少万元?(本小题满分10分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com