
2006-2007年烟台市招远第二学期期末考试
初三数学试题
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分。
整个试卷满分为120分。
一、选择题:(将唯一正确答案代号填在括号内。每小题2分,满分30分)
1.下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积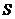 与边长
与边长 的关系
的关系
B.正方形的周长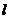 与边长
与边长 的关系
的关系
C.矩形的长为 ,宽为20,其面积
,宽为20,其面积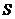 与
与 的关系
的关系
D.矩形的面积为40,长 与宽
与宽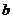 之间的关系
之间的关系
2.方程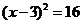 的根是( )
的根是( )
A.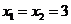 B.
B.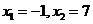
C.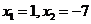 D.
D.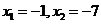
3.下列命题中,逆命题是假命题的是( )
A.若两个角的和为90°,则它们互为余角
B.两锐角的和为90°的三角形是直角三角形
C.有一个外角是直角的三角形是直角三角形
D.等边三角形是等腰三角形
4.如图,平面上两棵不同高度、笔直的小树,同一时刻在太阳光线照射下形成的影子分别是AB、DC,则( )

A.四边形ABCD是平行四边形 B.四边形ABCD是梯形
C.线段AB与线段CD相交 D.以上三个选项均有可能
5.在施掷一枚均匀的硬币的试验中,某一小组作了500次试验,当出现正面的频数是多少时,其出现正面的频率才是49.6%( )
A.248 B.
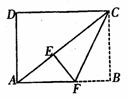
6.如图,在矩形ABCD中,AD=3,AB=4,将 ABC沿CF折叠,点B落在AC上的点E处,则
ABC沿CF折叠,点B落在AC上的点E处,则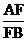 等于( )
等于( )
A. B.
B.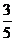 C.
C.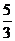 D.2
D.2
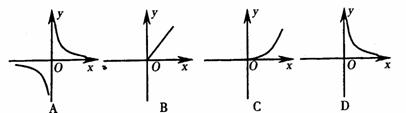
7.某果农苹果的总产量是9.3×104千克,设平均每棵苹果产 千克,苹果总共有
千克,苹果总共有 棵,则
棵,则 与
与 之间的函数关系图像大致是( )
之间的函数关系图像大致是( )
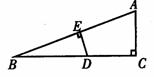
8.如图,在△ABC中, C=90°,
C=90°, ABC=15°,点D、E分别在BC、AB上,且DE垂直平分AB,BD=3,则DC等于( )
ABC=15°,点D、E分别在BC、AB上,且DE垂直平分AB,BD=3,则DC等于( )
A.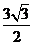 B.
B. 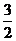 C.3 D.
C.3 D.
9.四条线段的长分别是2、4、6、8,从中任意取出三条线段,能围成三角形的概率是( )
A. B.
B. C.
C. D.
D.
10.将5个边长都为
A.
11.已知点A(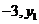 )、B(
)、B( )、C(
)、C(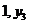 )都在函数
)都在函数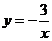 的图像上,则
的图像上,则 、
、 、
、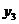 的大小关系是( )
的大小关系是( )
A. >
> >
>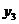 B.
B. >
> >
>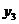
C. >
>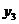 >
> D.
D.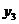 >
> >
>
12.在一幅长 cm,那么
cm,那么 满足的方程是( )
满足的方程是( )

A.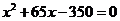 B.
B.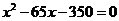
C. D.
D.
13.如图,两个转盘分别被分成3等份和4等份,分别标有数字1、2、3和1、2、3、4,转动两个转盘各一次(假定每次都能确定指针所指的数字),两次指针所指的数字之和为3或5的概率是

A. B.
B. C.
C.  D.
D.
14.如图,梯形ABCD中,AD//BC,BC=3AD,E是DC中点,则S△ADE:S△ABE为( )

A. B.
B. C.
C. D.
D.
15.函数 与
与 (
( )在同一直角坐标系中的图像可能是( )
)在同一直角坐标系中的图像可能是( )

二、填空题:(将正确答案填在横线上。每小题3分,满分30分)
16.如图,E、F是 ABCD的对角线BD上两点,且DE=BF。若
ABCD的对角线BD上两点,且DE=BF。若 AED=110°,
AED=110°, ABD=
ABD= ,则
,则 DCF的度数为 。
DCF的度数为 。

17.若方程 有两个不相等的实根,则
有两个不相等的实根,则 的取值范围是
。
的取值范围是
。
18.某花木场有一块形状为等腰梯形的空地(如图),各边的中点分别是E、F、G、H,测得对角线AC=

19.若反比例函数的图像经过点(一1,3),则其表达式为 。
20.一个不透明的盒子里装有5个黄球,2个红球,2个白球,除颜色不同外其余都相同,从中任意摸出一球是黄球的概率为 。
21.已知双曲线 分别位于第二、四象限,那么点
分别位于第二、四象限,那么点 一定在第 象限
一定在第 象限
22.如图,D是等边 ABC的边AC的中点,点E在BC的延长线上,CE=CD,若S△ABC=
ABC的边AC的中点,点E在BC的延长线上,CE=CD,若S△ABC= cm2,则
cm2,则 BDE的周长是
。
BDE的周长是
。

23.如图, ABC中,AD
ABC中,AD BC于D,E、F分别是AB、AC边的中点,连结DE、EF、FD,当
BC于D,E、F分别是AB、AC边的中点,连结DE、EF、FD,当 ABC满足 时,四边形AEDF是菱形(填写一个你认为恰当的条件即可)。
ABC满足 时,四边形AEDF是菱形(填写一个你认为恰当的条件即可)。

24.一张存折的密码由6个数字组成,每个数字都是0~9这十个数字中的一个,只有当6个数字与所设定的密码相同时,才能将款取出。粗心的王师傅记不清最后两个数字,但他知道这两个数字都不是“
25.若方程 的两根恰好是一直角三角形两条直角边的长,则此直角三角形的斜边长是 。
的两根恰好是一直角三角形两条直角边的长,则此直角三角形的斜边长是 。
三、解答题:(每小题8分,满分l6分)
26.已知函数 ,
, 与
与 成正比例,
成正比例, 与
与 成反比例,且当
成反比例,且当 =1时,
=1时, =4;当
=4;当 =2时,
=2时, =5。求
=5。求 与
与 的函数表达式。
的函数表达式。
27.如图,等腰梯形ABCD中,AB//CD,AB=2AD,梯形周长为40,对角线BD平分 ABC,求梯形的腰长及两底边的长。
ABC,求梯形的腰长及两底边的长。

四、操作与解释题:(满分9分)
28.将一张矩形纸按如图所示的方法折叠:

回答下列问题:
(1)图④中 AEF是多少度?为什么?
AEF是多少度?为什么?
(2)若AB=4,AD=6,CF=2,求BE的长。
五、实际应用题:(每小题10分,满分20分)
29.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光。

(1)任意闭合其中一个开关,求小灯泡发光的概率;
(2)任意闭合其中两个开关,请用画树状图或列表格的方法求出小灯泡发光的概率。
30.生产一种产品,需先将材料加热达到 (℃),从加热开始计算的时间为
(℃),从加热开始计算的时间为 (分钟)。据了解,该材料加热时,温度
(分钟)。据了解,该材料加热时,温度 与时间
与时间 成一次函数关系;停止加热进行操作时,温度
成一次函数关系;停止加热进行操作时,温度 与时间
与时间 成反比例关系(如图)。已知该材料在加热前的温度为
成反比例关系(如图)。已知该材料在加热前的温度为
(1)分别求出将材料加热和停止加热进行操作时, 与
与 的函数表达式;
的函数表达式;
(2)根据工艺要求,当材料的温度低于l

六、探索题:(满分l0分)
31.如图,正方形ABCD中,E是AD上一点(E与A、D不重合)。连接CE,将 CED绕点D顺时针旋转90°,得到
CED绕点D顺时针旋转90°,得到 AFD。
AFD。
(1)猜想CE和AF之间的关系,并进行证明。
(2)连接EF,若 ECD=30°,求
ECD=30°,求 AFE的度数。
AFE的度数。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com