
2008年甘肃省庆阳市中考
数学试题
友情提示:
1、抛物线 的顶点坐标是
的顶点坐标是 .
.
2、扇形面积公式为:S扇形= ;其中,n为扇形圆心角度数,R为扇形所在圆半径.
;其中,n为扇形圆心角度数,R为扇形所在圆半径.
3、圆锥侧面积公式:S侧= ;其中,r为圆锥底面圆半径,
;其中,r为圆锥底面圆半径, 为母线长.
为母线长.
一、选择题:本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一项是符合题目要求的,将此选项的代号填入题后的括号内.
1.化简: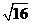 =( )
=( )
A.8 B.
2.下面四张扑克牌中,图案属于中心对称的是图中的( )

3.两圆半径分别为3和4,圆心距为7,则这两个圆( )
A.外切 B.相交 C.相离 D.内切
4.下列说法中,正确的是( )
A.买一张电影票,座位号一定是偶数
B.投掷一枚均匀的一元硬币,有国徽的一面一定朝上
C.三条任意长的线段都可以组成一个三角形
D.从1、2、3这三个数字中任取一个数,取得奇数的可能性大
5.正方形网格中, 如图放置,则
如图放置,则 =( )
=( )

A. B.
B. C.
C. D.
D.
6.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为 ,那么口袋中球的总数为( )
,那么口袋中球的总数为( )
A.12个 B.9个 C.6个 D.3个
7.如图,身高为 米的某学生想测量学校旗杆的高度,当他站在
米的某学生想测量学校旗杆的高度,当他站在 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=
处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=

A. 米 B.
米 B.
8.某商品经过两次连续降价,每件售价由原来的55元降到了35元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.55 (1+x)2=35 B.35(1+x)2=55
C.55 (1-x)2=35 D.35(1-x)2=55
9.如图, 是⊙
是⊙ 的直径,
的直径,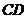 为弦,
为弦,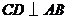 于
于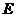 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.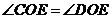 B.
B.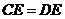 C.
C.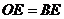 D.
D. =
=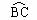
10.若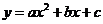 ,则由表格中信息可知
,则由表格中信息可知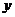 与
与 之间的函数关系式是( )
之间的函数关系式是( )

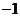
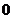

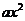




A. B.
B.
C. D.
D.
二、填空题:本大题共10小题,每小题4分,共40分.把答案填在题中的横线上.
11.方程 的解是
.
的解是
.
12.要使 在实数范围内有意义,
在实数范围内有意义, 应满足的条件是
.
应满足的条件是
.
13.“明天下雨的概率为
14.二次函数 的最小值是
.
的最小值是
.
15.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小
(填 “相同”、“不一定相同”、“不相同”之一).
16.两个相似三角形的面积比S1:S2与它们对应高之比h1:h2之间的关系为 .
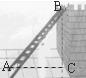
17.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离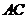 =
=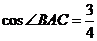 ,则梯子长AB = 米.
,则梯子长AB = 米.
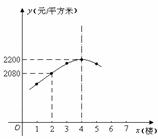
18.兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图像上(如图所示),则6楼房子的价格为 元/平方米.
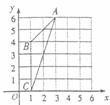
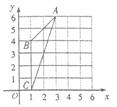
19.如图中 外接圆的圆心坐标是 .
外接圆的圆心坐标是 .
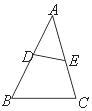
20.如图,D、E分别是 的边AB、AC上的点,则使
的边AB、AC上的点,则使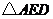 ∽
∽ 的条件是 .
的条件是 .
三、解答题(一):本大题共5小题,共38分.解答时,应写出必要的文字说明、证明过程或演算步骤.
21.(6分)计算: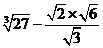 .
.
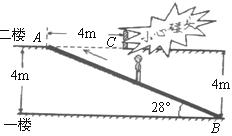
22.(7分)如图,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高
23.(7分)下图是某几何体的展开图.

(1)这个几何体的名称是 ;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(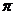 取3.14)
取3.14)
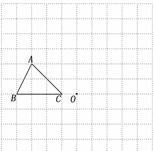
24.(8分)在如图的方格纸中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).
(1) 画出 绕点
绕点 顺时针旋转
顺时针旋转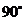 后的
后的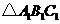 ;
;
(2)求点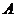 旋转到
旋转到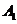 所经过的路线长.
所经过的路线长.
25.(10分)如图,线段 与⊙
与⊙ 相切于点
相切于点 ,连结
,连结 、
、 ,OB交⊙
,OB交⊙ 于点D,已知
于点D,已知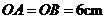 ,
, .求:(1)⊙
.求:(1)⊙ 的半径;(2)图中阴影部分的面积.
的半径;(2)图中阴影部分的面积.

四、解答题(二):本大题共4小题,共42分.解答时,应写出必要的文字说明、证明过程或演算步骤.
26.(10分)如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为 的无盖长方体箱子,且此长方体箱子的底面长比宽多
的无盖长方体箱子,且此长方体箱子的底面长比宽多

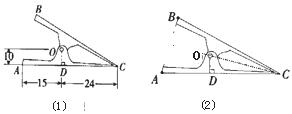
27.(10分)下图(1)是夹文件用的铁(塑料)夹子在常态下的侧面示意图. 表示铁夹的两个面,
表示铁夹的两个面, 点是轴,
点是轴, 于
于 .已知
.已知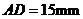 ,
, ,
, .已知文件夹是轴对称图形,试利用图(2),求图(1)中
.已知文件夹是轴对称图形,试利用图(2),求图(1)中 两点的距离(
两点的距离( )
)
28.(10分) 甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市:
球
两红
一红一白
两白
礼金券(元)
5
10
5
乙超市:
球
两红
一红一白
两白
礼金券(元)
10
5
10
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
29. (12分)一条抛物线 经过点
经过点 与
与 .
.
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1、圆心 在抛物线上运动的动圆,当⊙
在抛物线上运动的动圆,当⊙ 与坐标轴相切时,求圆心
与坐标轴相切时,求圆心 的坐标;
的坐标;
(3)⊙ 能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线
能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线 使⊙
使⊙ 与两坐标轴都相切(要说明平移方法).
与两坐标轴都相切(要说明平移方法).
附加题:15分
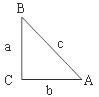
1.(6分)如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则
sinA=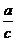 , cosA=
, cosA=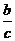 ,tanA=
,tanA=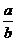 .
.
我们不难发现:sin260o+cos260o=1,… 试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
2.(9分)对于本试卷第19题:“图中 外接圆的圆心坐标是 .”
外接圆的圆心坐标是 .”
请再求:(1) 该圆圆心到弦AC的距离;
(2)以BC为旋转轴,将 旋转一周所得几何体的全面积(所有表面面积之和).
旋转一周所得几何体的全面积(所有表面面积之和).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com