
2008年江苏省启东中学中考模拟考试(五)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)
1.在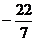 ,
,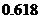 ,
,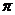 ,
,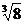 ,
,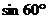 中,无理数的个数是
中,无理数的个数是
A.1个 B.2个 C.3个 D.4个
2.已知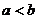 ,下列四个不等式中,不正确的是
,下列四个不等式中,不正确的是
A.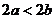 B.
B.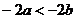
C.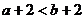 D.
D.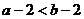
3.图1是一个正在绘制的扇形统计图,整个圆表示某班参加体育活动的总人数,那么表示参加立定跳远训练的人数占总人数的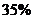 的扇形是
的扇形是
A.M B.N C.P D.Q
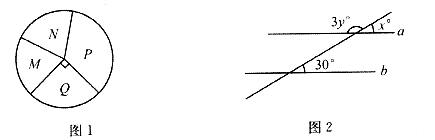
4.如图2所示,直线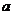 与直线
与直线 互相平行,则
互相平行,则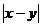 的值是
的值是
A.20 B.80 C.120 D.180
5.如图3所示,将一张长方形纸片对折两次,然后剪下一个角打开.如果要剪出一个正方形,那么剪口线与折痕成
A.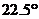 角
B.
角
B.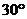 角
C.
角
C. 角 D.
角 D.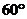 角
角

6.如图4所示,雷达可用于飞机导航,也可用来监测飞机的飞行.假设某时刻雷达同飞机发射电磁波,电磁波遇到飞机后反射,又被雷达接收,两个过程共用了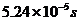 .已知电磁波的传播速度为
.已知电磁波的传播速度为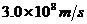 ,则该时刻飞机与雷达站的距离是
,则该时刻飞机与雷达站的距离是
A.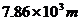 B.
B.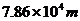
C.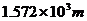 D.
D.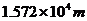
7.如下图5所示,半径为l的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为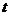 ,正方形除去圆部分的面积为S(阴影部分),则S与
,正方形除去圆部分的面积为S(阴影部分),则S与 的大致图像为
的大致图像为

8.在图6所示的图形中,既是中心对称又是轴对称的图形是
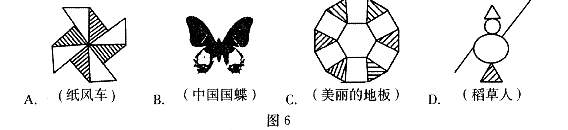
9.如图7所示,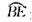 是半径为6的⊙D的
是半径为6的⊙D的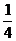 圆周,C点是
圆周,C点是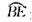 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是
A.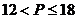 B.
B.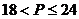
C.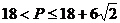 D.
D.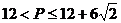

10.如图8所示,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第 个内切圆,它的半径是
个内切圆,它的半径是
A. B.
B.
C. D.
D.
第Ⅱ卷(共118分)
二、填空题(本大题共8小题,每小题3分,共24分,把答案填写在题中的横线上)
11.若分式 的值为零,则
的值为零,则 的值为 .
的值为 .
12.根据图9所示的程序,计算当输入 时,输出的结果
时,输出的结果 .
.

13.如图10所示,一根电线杆的接线柱部分AB在阳光下的投影CD的长为 ,则AB的长为 m(精确到
,则AB的长为 m(精确到
14.平面直角坐标系中有六个点A(1,5),B(-3, ),C(-5,-l),D(-2,
),C(-5,-l),D(-2, ),E(3,
),E(3, ),F(
),F( ,2),其中有五个点在同一反比例函数图像上,不在这个反比例函数图像上的点是 .
,2),其中有五个点在同一反比例函数图像上,不在这个反比例函数图像上的点是 .
15.从-1,1,2这三个数中,任取两个不同的数作为一次函数 的系数
的系数 ,
, ,则一次函数
,则一次函数 的图像不经过第四象限的概率是 .
的图像不经过第四象限的概率是 .
16.如图11,天秤中的物体a、b、c使天秤处于平衡状态,则质量最大的物体是 .

17.如图12所示,矩形ABCD中, ,
,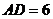 ,将矩形ABCD在直线
,将矩形ABCD在直线 上按顺时针方向不滑动地每秒转动
上按顺时针方向不滑动地每秒转动 ,转动3s后停止,则顶点A经过的路线长为 .
,转动3s后停止,则顶点A经过的路线长为 .
18.现有若干张边长不相等但都大于 角画线,将正方形纸片分成5部分,则中间阴影部分的面积是
角画线,将正方形纸片分成5部分,则中间阴影部分的面积是  ;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?
;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?

三、解答题(本大题共l0小题,共84分,解答应写出文字说明或演算步骤.)
19.(本题6分)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解.

20.(本题6分)解分式方程:
21.(本题8分)某人在电车路轨旁与路轨平行的路上骑车行走,他留意到每隔6分钟有一部电车从他后面驶向前面,每隔2分钟有一部电车从对面驶向后面.假设电车和此人行驶的速度都不变(分别为 ,
, ),请你根据下面的示意图,求电车每隔几分钟(用t
),请你根据下面的示意图,求电车每隔几分钟(用t

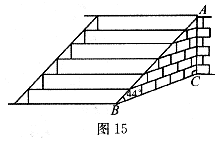
22.(本题8分)如图15所示,武当山风景管理区为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44º减至32º,已知原台阶AB的长为
(1)改善后的台阶会加长多少?(精确到
(2)改善后的台阶多占多长的一段地面?(精确到
23.(本题10分)元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:

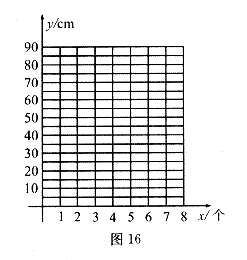
(1)把上表中 ,
,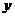 的各组对应值作为点的坐标,在如图16所示的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图16所示的平面直角坐标系中描出相应的点,猜想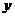 与
与 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
(2)教室天花板对角线长
24.(每小题6分,满分12分)
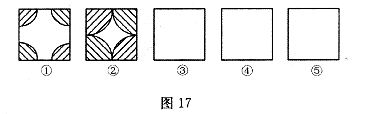
(1)为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案,既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出三种不同的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种。
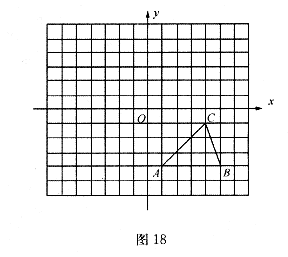
(2)如图18所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-l).
①把△ABC向上平移5个单位后得到对应的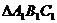 ,画出
,画出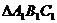 ,并写出点
,并写出点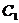 的坐标;
的坐标;
②以原点O为对称中心,再画出与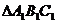 关于原点O对称的
关于原点O对称的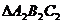 ,并写
,并写 的坐标。
的坐标。
25.(本题12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
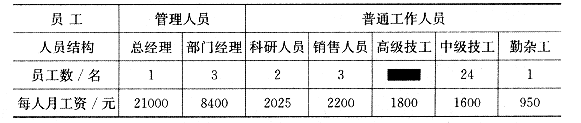
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名.
(2)所有员工月工资的平均数j为2500元,中位数为 元,众数为 元.
(3)小张到这家公司应聘普通工作人员.请你回答图19中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些.
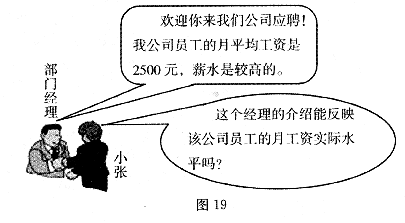
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资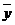 (结果保留整数),并判断
(结果保留整数),并判断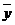 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
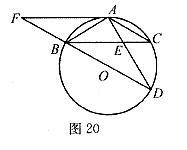
26.(本题10分)如图20所示,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
(1)求证: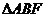 ∽
∽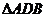 ,并求AB的长.
,并求AB的长.
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?为什么?
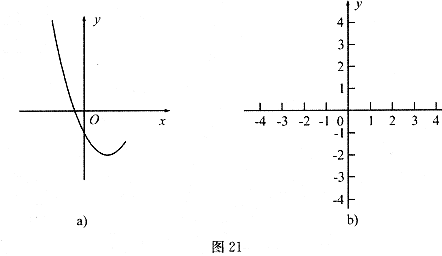
27.(本题12分)已知抛物线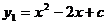 的部分图像如图
的部分图像如图
(1)求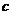 的取值范围.
的取值范围.
(2)若抛物线经过点(0,-l),试确定抛物线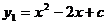 的解析式.
的解析式.
(3)若反比例函数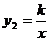 的图像经过(2)中抛物线上点(1,
的图像经过(2)中抛物线上点(1,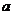 ),试在图21b所示的直角坐标系中,画出该反比例函数及(2)中抛物线的图像,并利用图像比较
),试在图21b所示的直角坐标系中,画出该反比例函数及(2)中抛物线的图像,并利用图像比较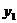 与
与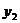 的大小.
的大小.
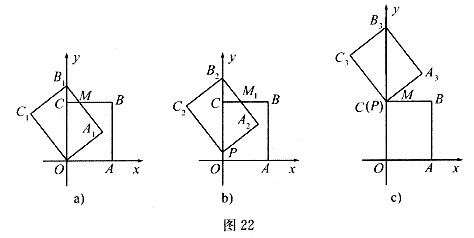
28.(本题14分)如图 轴、
轴、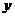 轴建立平面直角坐标系,A点的坐标为(3,0),C点的坐标为(0,4).将矩形OABC绕O点逆时针旋转,使B点落在y轴的正半轴上,旋转后的矩形为
轴建立平面直角坐标系,A点的坐标为(3,0),C点的坐标为(0,4).将矩形OABC绕O点逆时针旋转,使B点落在y轴的正半轴上,旋转后的矩形为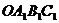 ,BC、
,BC、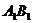 ,相交于点M.
,相交于点M.
(1)求点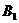 的坐标与线段
的坐标与线段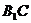 的长;
的长;
(2)将图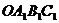 沿
沿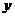 轴向上平移,如图b,矩形
轴向上平移,如图b,矩形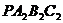 是平移过程中的某一位置,BC、
是平移过程中的某一位置,BC、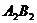 相交于点
相交于点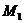 ,点P运动到C点停止.设点P运动的距离为
,点P运动到C点停止.设点P运动的距离为 ,矩形
,矩形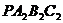 与原矩形OABC重叠部分的面积为
与原矩形OABC重叠部分的面积为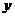 ,求
,求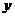 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如图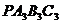 .请你思考如何通过图形变换使矩形
.请你思考如何通过图形变换使矩形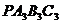 与原矩形OABC重合,请简述你的做法.
与原矩形OABC重合,请简述你的做法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com