
2007-2008学年度菏泽市定陶县第二学期九年级期中学业水平测试
数学题样
一、选择题:(本题共12个小题,每小题3分,在所给的四个选项中,只有一个选项是正确的,多选、不选均记0分)
1.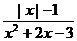 的值为0,则
的值为0,则 的值为__________
的值为__________
A.±l
B.
2. =__________
=__________
A.2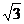 +2 B.2
+2 B.2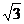 一
一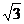 D.2
D.2
3.我国耕地面积为ll5400000亩,用科学记数法保留2个有效数字________
A.1.2×108 B.1.1×
4.若点M的坐标为(3 sin45°,cos30°),则点M关于原点对称点的坐标为_________
sin45°,cos30°),则点M关于原点对称点的坐标为_________
A.(3,一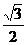 ) B.(一3,
) B.(一3,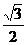 ) C.(-3,一
) C.(-3,一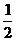 ) D.(一3,一
) D.(一3,一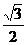 )
)
5.在△ABC中,∠A=65°,∠B=75°,将纸片一角折叠,点C落在△ABC内,若∠1=60°,则∠2为_________度
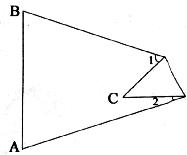
A.10° B.20° C.30° D.40°
6.已知:不等式组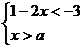 的解集为
的解集为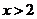 ,则_________
,则_________
A. <2 B.
<2 B. =
= >2 D.
>2 D. ≤2
≤2
7.已知:sin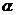 ?cos
?cos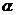 =
=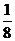 且45°<
且45°<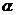 <90°则cos
<90°则cos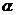 -sin
-sin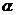 的值为_____________
的值为_____________
A.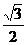 B.-
B.-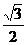 C.
C.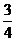 D.-
D.-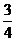
8.如图:由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数为__________
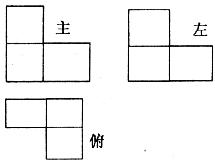
A.3个 B.4个 C.5个 D.6个
9.某商店在一次买卖中同时卖出两件上衣,每件都以135元卖出,若按成本计算其中一件盈利25%,另一件则亏损25%,则这家商店在这次买卖中_________
A.不赔不赚 B.赚9元 C.赔9元 D.赔18元
10.在正方形网格中,每个小方格都是边长为1的正方形,AB两点在方格的顶点上如图:点C也在方格顶点上且△ABC面积为1个单位,则符合条件的C点个数为_________
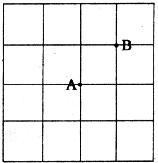
A.3
B.
11.如图:王华晚上由路灯A下的B处走到C处时测得影长CD为

A.
12.在菱形ABCD中,∠A=135°AB= ,以点C为圆心的弧EF分别与AB、AD相切于点G、H,与BC、CD分别交于点E、F,用扇形CEF作圆锥的侧面,则这个圆锥的高为________
,以点C为圆心的弧EF分别与AB、AD相切于点G、H,与BC、CD分别交于点E、F,用扇形CEF作圆锥的侧面,则这个圆锥的高为________

A. B.
B. C.
C. D.
D.
二、填空题:(本题共l0个小题,每小题3分,共30分,只要求填写最后结果)
13.已知:抛物线 顶点在
顶点在 轴上,则b为____________.
轴上,则b为____________.
14.若⊙A与⊙B相切,它们的半径分别为
15.用 定义新运算:对于任意实数a、b都有a
定义新运算:对于任意实数a、b都有a b=b2+1例如:7
b=b2+1例如:7 4=42+1=17则5
4=42+1=17则5 3=________.当m为实数时,m
3=________.当m为实数时,m (m
(m 2)=__________.
2)=__________.
16.一组数据了 、
、 、
、 、
、 ……请按这种规律,写出第7个数据_____________.
……请按这种规律,写出第7个数据_____________.
17.商店销售一种纪念品,进价为4元,根据调查,单价为l0元时,销售量为200个,而单价每降1元,就可多售50个,当销售单价为________元时,获得利润最大.
18.直线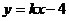 与
与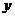 轴相交所成锐角的正切值为
轴相交所成锐角的正切值为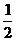 ,则
,则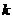 =_________.
=_________.
19.锐角△ABC中.若(sinA-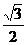 )2+|cosB-
)2+|cosB-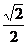 |=0,则∠C=____________度。
|=0,则∠C=____________度。
20.如图为某种型号的正六角形,螺母的三视图,则它的表面积为__________.
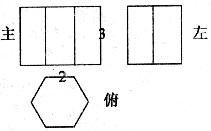
21.在平面直角坐标系中,已知:P0(1,0)将点P0绕着原点O逆时针方向旋转60°得到点P1,延长OP1到P2,使OP2=2OP1,再将点P2绕原点O按逆时针旋转60°得到点P3,则点P3的坐标为___________.
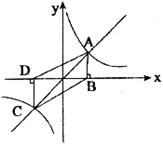
22.正比例函数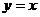 与反比例函数
与反比例函数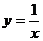 的图像交于A、C两点.AB⊥
的图像交于A、C两点.AB⊥ 轴于B点,CD⊥
轴于B点,CD⊥ 轴于D点,则四边形ABCD的面积是__________。
轴于D点,则四边形ABCD的面积是__________。
三、解答题:(本大题共54分)
23.已知: +b=2008
+b=2008  b=2008,求:
b=2008,求: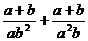 的值?(5分)
的值?(5分)
24.解方程: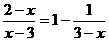 (5分)
(5分)
25.设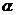 为锐角,且有2cos2
为锐角,且有2cos2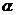 一5sin
一5sin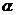 +1=0,求
+1=0,求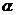 的值?(4分)
的值?(4分)
26.北京08奥运会吉祥物“贝贝、京京、欢欢、迎迎、妮妮”现在将三张分别写有“迎迎、欢欢、妮妮”这个吉祥物图案的卡片(形状大小质地完全相同)放入盒子.
求:(1)小玲从盒中任取一张,取到“欢欢”的概率多大?
(2)小玲从盒中取一张卡片,记下名字再放回,再从盒中取一张,记下名字,请用列表或画树状图列出小玲取到的所有可能情况?并求出两次都取到欢欢的概率.(6分)
27.已知直角三角形两个锐角的正弦sinA、sinB是方程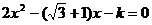 的两个根.
的两个根.
求:∠A、∠B和K值?(6分)
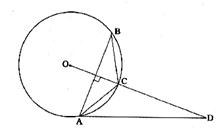
28.如图:△ABC内接于⊙O,点D在⊙C的延长线上.sinB=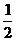 ,∠CAD=30°
,∠CAD=30°
求:(1)AD为⊙O切线?(4分)
(2)若OD⊥AB,BC=5,求AD的长?(4分)
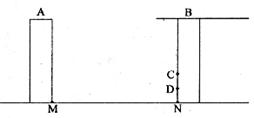
29.某居民小区AB两楼之间的距离MN=
(参考数据: =1.414
=1.414 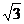 =1.732
=1.732 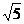 =2.236)
=2.236)
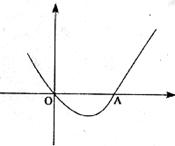
30.(12分)已知:如图,二次函数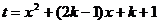 的图象与
的图象与 轴相交于O、A两点
轴相交于O、A两点
求:(1)这个二次函数的解析式?
(2)在这条抛物线对称轴右边的图象上有一点B,使锐角△AOB的面积等于3,求点B的坐标?
(3)对于②中的点B,在抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标?并求出APOB的面积? 若不存在,请说明理由?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com