
2008年阳谷县中考适应性训练(五)
数学试卷
(时间:120分钟,满分:150分)
一、选择题(每题4分,共60分)
1.下列运算正确的是
A.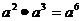 B.
B.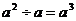
C.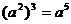 D.
D.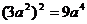
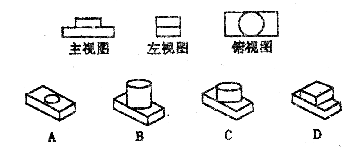
2.下列三视图所对应的直观图是
3.下列四个函数,当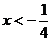 时,y 随 x的增大丽减小的函数是
时,y 随 x的增大丽减小的函数是
A.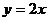 B.
B.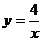
C.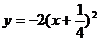 D.
D.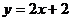
4.将不等式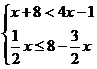 的解集在数轴上表示出来,正确的是
的解集在数轴上表示出来,正确的是
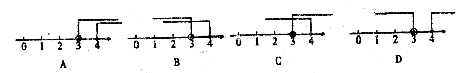
5.小华有蓝色和红色的运动装备一套,他任意找出一件上衣和一条裤子,那么他所找出的上衣和裤子恰恰配成一套的概率为
A.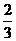 B.
B.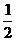 C.
C.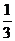 D.
D.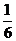
6.两圆⊙O1,和⊙O2的直径分别为4和6,O1、O2的坐标分别是(0,3)、(4,0),那么两圆的位置关系是
A.外切 B.相交 C.内切 D.外离
7.已知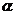 为锐角,
为锐角,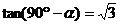 ,则
,则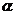 的度数为
的度数为
A.30º B.45º C.60º D.75º
8.下列图形中,中心对称图形是
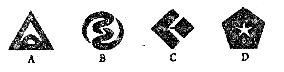
9.如图,⊙M与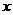 轴相切于原点,平行于
轴相切于原点,平行于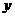 轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是
轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是
A.(0,3) B.(0,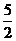 )
)
C.(0,2) D.(0,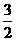 )
)

10.下列五个命题中,真命题的个数是
①零是最小的实数;②数轴上的所有点都表示实数;③无理数就是带根号的数;④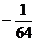 的立方根是
的立方根是 ;⑤一个实数的平方根有两个,它们互为相反数。
;⑤一个实数的平方根有两个,它们互为相反数。
A.1 B.2 C.3 D.4
11.小明一家人周六去荷塘月色游玩,早上8┱00出发,行走速度是
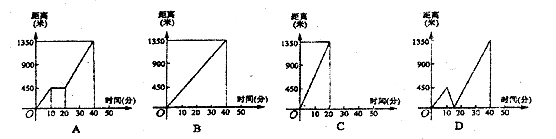
12.已知二次函数 的图像如图所示,则a、b、c满足
的图像如图所示,则a、b、c满足
A. B.
B.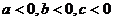
C.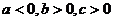 D.
D.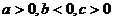
13.将AABC的三个顶点坐标的横坐标乘以-l,纵坐标不变,则所得图形与原图形的关系是
A.关于 轴对称
B.关于
轴对称
B.关于 轴对称
轴对称
C.关于原点对称 D.将原图向x轴的负方向平移1个单位
14.如图所示的图形由两个正三角形叠合而成,其中多边形ABC-DEF是正六边形,其面积为l,则阴影部分的面积为
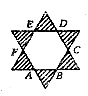
A.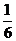 B.
B.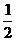
C.1 D.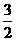
15.如图.在△ABC,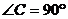 ,
,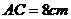 ,
,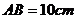 ,点P由C出发以每秒
,点P由C出发以每秒
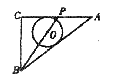
A.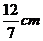 B.
B.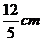
C.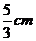 D.
D.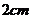
二、填空题(每小题4分,共20分)
16.在半径为1的圆中,有两条弦,其中A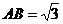 ,
,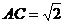 ,则
,则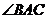 的度数是 。
的度数是 。
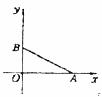
17.如图,若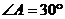 ,点B的坐标为(0,2),把△AOB绕点O按逆时针方向旋转90º,则这时边AB的中点的坐标为 。
,点B的坐标为(0,2),把△AOB绕点O按逆时针方向旋转90º,则这时边AB的中点的坐标为 。
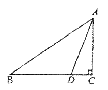
18.如图所示,△ABC中,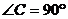 ,点D在BC上,且DB=DA,
,点D在BC上,且DB=DA,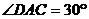 ,则
,则 。
。
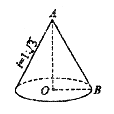
19.如图,某公园计划在一座圆锥形土丘上铺满草皮,如图所示,土丘高为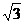 ,则草皮面积为
,则草皮面积为 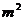 。
。
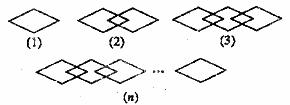
20.找规律:如下图,第(1)幅图中有1个菱形,第(2)幅图中有3个菱形,第(3)幅图中有5个菱形,则第(n)幅图中有 个菱形。
三、解答题(共70分)
21.(6分)已知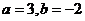 求:
求: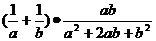 的值。
的值。
22.(8分)解方程: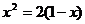
23.(8分)如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上一点,DE=B C。
(1)求证: ;
;
(2)判断 ACE的形状。(不需要说明理由)
ACE的形状。(不需要说明理由)
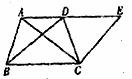
24.(10分)如图,AB是⊙O的直径,C是AB延长线上一点,CD切⊙O于D,过点B作⊙O的切线交CD于E,若AB=CD=2,求CE的长。
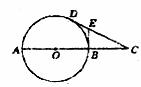
25.(12分)如图所示的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2:俯视图分别是A3、B3、C3。
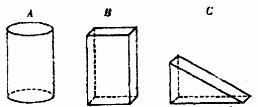
(1)请你分别写出A1、A2、A3;B1、B2、B3;C1、C2、C3图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A1、A2、A3,的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片。
①通过补全下面的树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
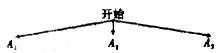
②小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称拥同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜,这个游戏对双方公平吗?为什么?
26.(12分)某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高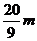 ,与篮圈中心的水平距离为
,与篮圈中心的水平距离为
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面
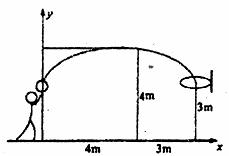
27.(14分)如图①,在直角坐标系中,点A的坐标为(1,0),,以OA为边在第四象限内作等边△AOB,点C为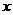 轴的正半轴土一动点(OC>1),连结BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E。
轴的正半轴土一动点(OC>1),连结BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E。
(1)试问△OBC与△ABD全等吗?并证明你的结论。
(2)随着点C位置的变化,点E的位置是否发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由。
(3)如图②,以OC为直径作圆,与直线DE分别交于点F、G,设AG=m。AF=n,用含n的代数式表示m(提示:连结OG、OF、FC)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com