
2007-2008学年度莘县第一学期学业水平统一检测
九年级数学试题
试题共4页,满分120分,考试时间100分钟。
一、选择题(本大题共15个小题,每小题4分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列图形中.既是轴对称图形又是中心对称图形的是
A.等边三角形 B.菱形 C.正五边形 D.等腰梯形
2.若分式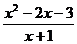 的值为零,则
的值为零,则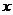 的值为
的值为
A.-l B.3 C.-1或3 D.-3或1
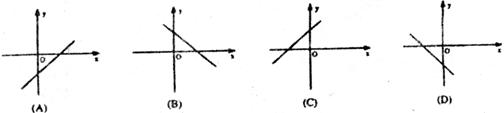
3.已知一次函数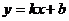 中,
中,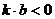 ,且
,且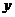 随
随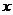 的增大而减小,则它的图像是
的增大而减小,则它的图像是
4.已知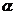 为锐角,
为锐角,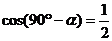 ,则
,则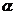 的度数为
的度数为
A.30° B.45° C.60° D.90°
5.如果两个圆的半径分别为
A.外离 B.外切 C.相交 D.内切
6.如下图,顺次连结四边形ABCD各边中点得四边形EFGH,要使EFGH是菱形,应添加的条件是
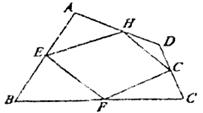
A.AD∥BC B.AC=BC C.AC=BD D.AD=AB
7.如下图,以直角坐标系的原点O为圆心,以1为半径作圆,若点P是该圆上第一象限内一点,且OP与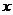 轴正方向组成的角为
轴正方向组成的角为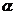 ,则P点的坐标为
,则P点的坐标为

A.(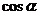 ,1)
B.(1,
,1)
B.(1,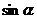 )
)
C.(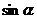 ,
,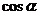 ) D.(
) D.(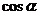 ,
,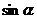 )
)
8.在Rt△ABC中,∠C=90°,若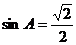 ,则cosB=
,则cosB=
A.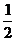 B.
B.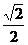 C.
C.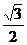 D.1
D.1
9.已知抛物线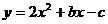 的顶点坐标为(1,-3),则
的顶点坐标为(1,-3),则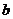 ,
,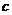 的值应为
的值应为
A.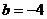 ,
,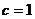 B.
B.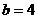 ,
,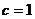
C.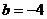 ,
,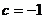 D.
D.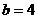 ,
,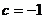
10.在Rt△ABC中,∠C=90°,∠A=30°,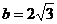 ,则此三角形外接圆的直径为
,则此三角形外接圆的直径为
A.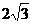 B.4 C.
B.4 C.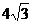 D.8
D.8
11.抛物线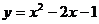 的顶点坐标是
的顶点坐标是
A.(1,-l) B.(-1,2) C.(1,-2) D.(-1,-2)
12.如果圆锥母线长为
A.9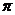 cm2 B.
cm2 B.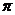 cm2 C.27
cm2 C.27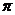 cm2 D.36
cm2 D.36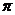 cm2
cm2
13.钟表的分针匀速旋转一周需要60分钟,现在的时间是中午l2:00点整,经过20分钟,分针与时针的夹角为
A.100° B.116° C.115° D.120°
14.在平面直角坐标系中,P(0,-3)是以原点为圆心,5为半径的圆内一点,那么经过点P的所有弦中,最短的弦长为
A.4 B.6 C.8 D.10
15.在平角直角坐标系中,已知点A(2,-2),在Y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共5个小题,每小题4分,共20分,只要求填写最后结果)
16.当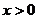 时,函数
时,函数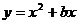 随
随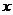 的增大而增大,则
的增大而增大,则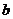 的取值范围是 。
的取值范围是 。
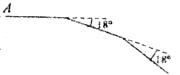
17.如图某同学从A点出发前进10m,向右转18°,再前进10m,又向右转l8°,这样一直走下去,他第一次回到出发点A时,一共走了 m。
18.函数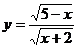 中,自变量
中,自变量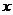 的取值范函是 。
的取值范函是 。
19.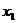 ,
,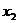 是方程
是方程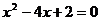 的两个根,则
的两个根,则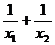 的值为 。
的值为 。
20.研究下列算式,你会发现有什么规律?
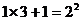
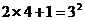

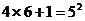
……
请将你找出的规律用公式表示出来 。
三、解答题(本大题共5个小题,共40分。解答应写出必要的文字说明、推理过程或演算步骤)
21.计算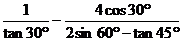 (4分)
(4分)
22.甲、乙两楼相距36米,从乙楼底B望甲楼顶C的仰角为45°,从甲楼顶C望乙楼顶D的俯角为30°,求两楼的高AC、BD各为多少米?(精确到1米,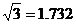 ,
,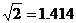 )(9分)
)(9分)

23.某种商品,按标价销售每件可盈利50元,平均每天销售24件,根据市场信息,若每件商品每降价1元,则每天可多销售3件。如果经销商想保证每天盈利2160元,同时考虑不过分增加营业员的工作量,每件应降低多少元?(9分)
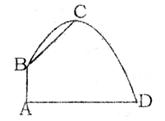
24.已知如图,AB是⊙O直径,CD是⊙O的切线,D为切点,AC⊥CD于C,AC交⊙O于点E,CD与AB的延长线交于点F。(9分)
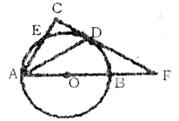
求证: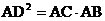
25.一自动喷灌设备的喷流情况如图,设水管AB在高出地面1.5m的B处有一自动旋转的喷水头,喷出的水流是抛物线的形状,喷头B与水流最高点C的连线和竖直方向成45°角,水流最高点C比喷头B高2m,求水流落点D到A点的距离。(9分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com